問題ＰＤＦ
四角形ＡＢＣＤは正方形で、点Ｐは辺ＡＢ上の点、点Ｑは辺ＡＤ上の点とします。
さらにＣＰとＢＱは垂直に交わっており、その交点をＲとします。
また、点Ｒから辺ＡＢに引いた垂線をＲＳとします。ＢＱとＤＰの交点をＴとします。
いまＰＲ＝585ｃｍ、ＣＲ＝1040ｃｍ、ＱＲ＝845ｃｍ、ＱＴ＝125ｃｍ、ＲＳ＝468ｃｍです。
次の問いに答えなさい。
（１）
ＢＲの長さを求めなさい。
（２）
正方形ＡＢＣＤの１辺の長さを求めなさい。
（３）
三角形ＤＱＴの面積を求めなさい。
＠解説＠
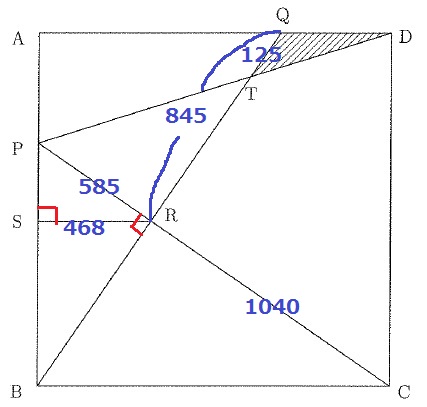
数値がデカイ!!( ;ﾟдﾟ)
パッと見て、ＢＲより正方形の一辺であるＢＣの方が求めやすい。
△ＰＳＲと△ＰＢＣの相似から、ＢＣ＝468×（585＋1040）/585＝1300
（２）正方形の一辺…1300ｃｍ
（１）
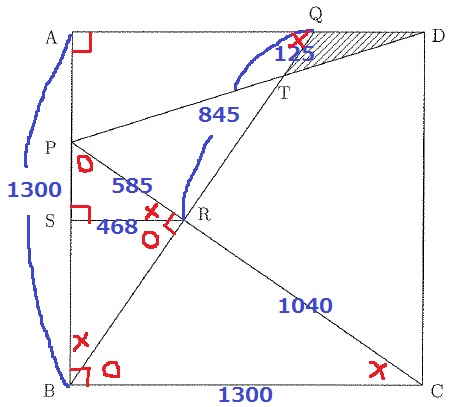
○＋×＝90°として、角度を調査。
△ＰＣＢと△ＱＢＡに着目すると、一辺と両端角が等しく合同。
ＰＣ＝ＱＢなので、ＱＢ＝585＋1040＝1625ｃｍ
ＢＲ＝ＱＢ－ＱＲ＝1625－845＝780ｃｍ
（３）
△ＡＱＢと△ＳＲＢの相似から、
ＡＱ＝468×1625/780＝975ｃｍ
ＱＤ＝1300－975＝325ｃｍ
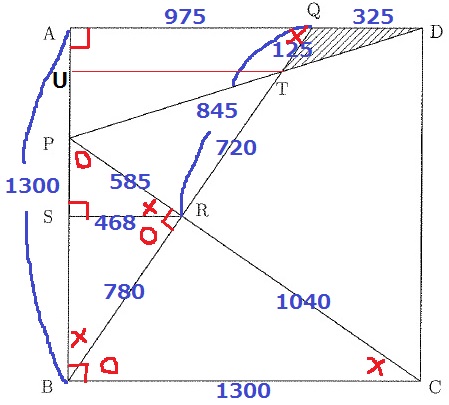
ＴからＡＢに向けて垂線をひき、交点をＵとする。
ＡＵ：ＵＢ＝ＱＴ：ＴＢ＝125：845－125＋780＝125：1500＝１：12
ＡＵ＝1300×１/13＝100ｃｍ
よって、△ＤＱＴの面積は、325×100÷２＝16250ｃｍ2
*ちなみに、相似である直角三角形の辺をがんばって約分すると辺の比は３：４：５になる。
難関中（算数科）解説ページに戻る
コメント