2018年度　東海中学過去問【算数】大問３解説

問題ＰＤＦ
２つの水そうＡ、Ｂに、はじめ10：７の割合で水が入っています。
Ａに毎分１Ｌずつ、Ｂに毎分0.5Ｌずつの水を入れたところ、
いっぱいになるまでにかかった時間は同じでした。
２つの水そうＡ，Ｂの容積の比は15：８です。
（１）
水そうＢについて、はじめに入っていた水の量と、
いっぱいになったときに入っていた水の量の比を求めなさい。

（２）
ＡとＢの容積の合計が460Ｌのとき、
いっぱいになるまでにかかった時間を求めなさい。

＠解説＠
（１）
水槽ＡとＢは容積が15：８、初めの水の量が10：７
空いたスペースに２：１の水量で入れていくと、
同じ時間で満水になったということは、空いたスペースの体積比は２：１

↑図で示すとこのような感じ。あとは消去算。

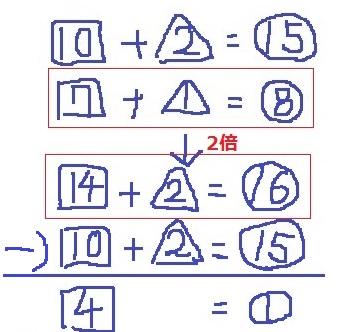
①＝□４
○を４倍すると□になる。

水槽Ｂではじめに入っていた水の量と、いっぱいになったときの水の量は７：32

（２）
前問が正解できればサービス問題。
水槽ＡとＢの容積比→□60：□32
この合計が460Ｌにあたる。
Ａの△２（空いたスペース）は、□60－□10＝□50に相当するので、
□50＝460×50/92＝250Ｌ
Ａには毎分１Ｌずつ水をいれるから250分かかる。
難関中（算数科）解説ページに戻る