問題PDF
<図1>のように、立方体ABCD-EFGHにおいて、
辺AB、辺FG、辺GHの真ん中の点をそれぞれI、J、Kとし、
点I、J、Kを通る面でこの立体を切ったときにできる面を(あ)とします。
(1)
点A、F、Hを通る面でこの立方体を切ったときにできる面を(い)とします。
このとき、(い)の面積は(あ)の面積の何倍ですか。
(2)

立方体の面EFGHについて、<図2>のそれぞれの辺の上の点は、
辺を4等分した点を表しています。
このとき、<図3>のように、正方形LMNOを底面とする直方体を立方体からくりぬきます。
点I、J、Kを通る面でこの立体を切ったときにできる面を(う)とします。
このとき、(う)の面積は(あ)の面積の何倍ですか。
(3)

立方体の面CGHDについて、<図4>のそれぞれの辺の上の点は、
辺を4等分した点を表しています。
このとき、<図5>のように、(2)で直方体をくりぬいてできた立体から
正方形PQRSを底面とする直方体をくりぬきます。
点I、J、Kを通る面でこの立体を切ったときにできる面を(え)とします。
このとき、(え)の面積は(あ)の面積の何倍ですか。
@解説@
(1)

I・J・Kを通る切断は正六角形。
A・F・Hを通る切断は正三角形。
辺の比は、△JGK∽△FGHからJK:FH=①:②
小さい正三角形の1辺の長さは①で同じ。面積比は小さい正三角形の個数で計算する。
(あ):(い)=6:4=3:2
よって、2/3倍。
(2)
なかの直方体の部分が空洞をつくる。

直方体の切断。
ポイントは、正六角形の切断面上にある直方体の頂点に注目すること!
上から見た図では、LとNがそれにあたる。
Nの真下、面EFGH上の点をN’とすると、Lから始まりN’で終わるように直方体を切断する。
すると、直方体の切断面は菱形になり、真ん中で切ると正三角形が2つ。
この正三角形の1辺はMOと同じ長さで、先ほどの①に等しい。
求積すべき斜線部分の面積は、正三角形6つから2つ分を取り除く。
よって、4/6=2/3倍
(3)
形がより複雑に(´゚д゚`)
だが、やることは前問と同様。
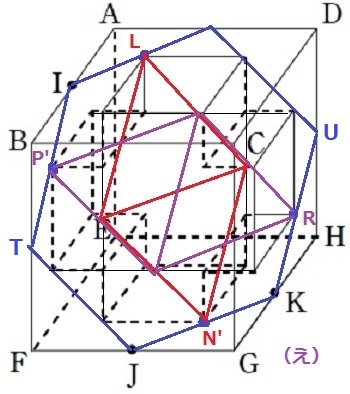
横の長方形がどう切断させるか。
辺IT(頂点P’)から辺UK(頂点R)に向かって切ってみよう。
前問と同じ菱形が現れる。
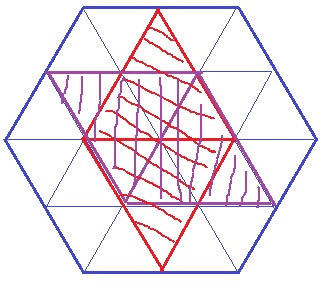
お馴染みの正六角形の分割。
斜線部分が空洞になるところ。
(え)の面積は、正三角形24個のうち14個。
よって、14/24=7/12倍



コメント