問題PDF
1からnまでの整数を次の2つの条件を満たすように並べます。
条件1 はじめの数は1
条件2 数が大きくなった後は小さくなり、小さくなった後は大きくなる
例えばnが4のとき、条件を満たす並べ方は1→3→2→4と1→4→2→3
の2通りがあります。このとき次の問いに答えなさい。
(1)
nが5のとき、条件を満たす並べ方は何通りありますか。
(2)(あ)
nが9のとき、1から9までの整数のうち最後の整数としてありえない整数をすべて求めなさい。
(い)
nが10のとき、1から10までの整数のうち最後の整数としてありえない整数をすべて求めなさい。
並んでいる数において、隣り合った数の差を(※)とします。
例えば1→3→2→4であれば、1と3の差は2、3と2の差は1、2と4の差は2となるので、
(※)に現れる数は1と2の2種類であり、(※)の和は2+1+2=5です。
(3)n=10のとき
(う)(※)の和の最大値は45です。
(※)の和が45となるような並べ方のうち、2番目が9であるような並べ方の例を1つ示しなさい。
(え)(※)の和の最小値は17です。
(※)の和が17とのあるような並べ方の例を1つ示しなさい。
(4)
nがどのような整数でも、うまく並べると(※)に現れる数を2種類にすることができます。
それぞれの場合に、その2種類の数を答えなさい。
(お)nが2019のとき
(か)nが2020のとき
@解説@
(1)

上がって下がって上がって下がる。
上がるときは下がるための着地点を残しておく必要があるので、
1の次は3・4・5のいずれか。
→5通り
(2)(あ)
出発は1なので、1は最後の整数にならない。
前問でn=5だと上り下りが偶数回なので、最後は下がる。
n=9も同様で最後は下がる。
ということは、最大数の9も最後にならない。
→1・9
(い)
n=10では上り下りが奇数回となるので、最後は上がる。
ということは、出発点の1を除いた最小値2は最後になりえない。
→1・2
(3)(う)
差の和を大きくするので落差をつける。
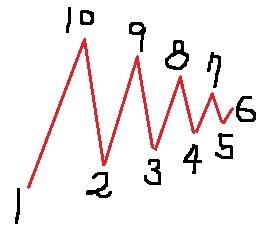
45が1~9の和なのでこういう形にしたいが、
問題文では『2番目が9』と条件が付けられている…。
が、上のような形を意識して数字を並べると解けてしまう。
1→9→2→10→3→8→4→7→5→6(例)
(え)
今度は落差を小さくさせる。

はじめは2歩進んで1歩下がる。
その後は3歩進んで1歩下がるを繰り返して10へ。
1→3→2→5→4→7→6→9→8→10(例)
(4)(お)
差を2種類に限定したい。
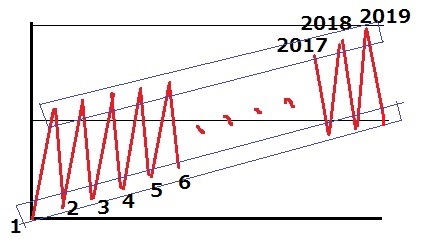
↑この図をイメージできるかどうか。
平行→2本の直線距離が同じ=差の種類が少なくなる。
上と下の数字の並びが平行関係にあればいい。
n=2019なので、最後は下がる。

上の列と下の列は数字がかぶってはいけないので、上のような順番になる。
すなわち、最後の数字は1~2019の中央値(2019+1)÷2=1010
1→1011→2→1012→3→1013………2018→1009→2019→1010
差は1010・1009・1010・1009・・をくり返す。
よって、1009と1010
(か)
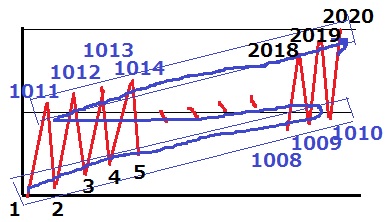
前問と同様。
ただし、n=2020とnが偶数なので最後は上がる。
差は1010・1009・1010・1009・・をくり返す。
1009と1010



コメント