問題PDF
8個の電球が円形に並んでいます。
次のルールにしたがってすべての電球が1秒ごとに点いたり消えたりします。
・電球Aが点いているとき
①両隣の電球がともに点いている場合は、Aは1秒後に消える。
②両隣の電球が1個または2個消えている場合は、Aは1秒後も点いたままである。
・電球Bが消えているとき
①両隣の電球が1個または2個消えている場合は、Bは1秒後も消えたままである。
②両隣の電球がともに点いている場合は、Bは1秒後に点く。
以下では、電球の状態を次のように表します。

例えば、図1のような電球の状態のとき、1秒後には図2のような電球の状態に変化します。
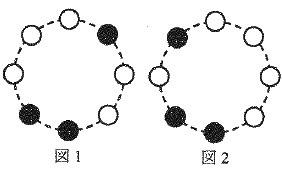
このとき、次の問いに答えなさい。
(1)
図3のような電球の状態のとき、1秒後の電球の状態をかきなさい。
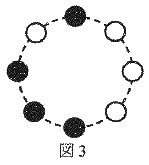
 (←解答用紙)
(←解答用紙)
(2)
何秒たっても位置も含めて電球の状態が変化しないとき、
考えられる最初の電球の状態をすべてかきなさい。
ただし、最初の電球の状態については、回転して同じ電球の状態になるものを1つとして考えなさい。
また、〔解答らん〕の使わなかった図には下の図4のように×をつけなさい。

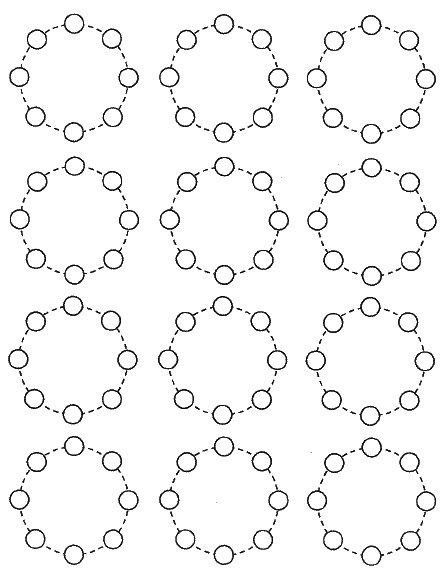 (←解答らん)
(←解答らん)
@解説@
(1)
ルールの確認。
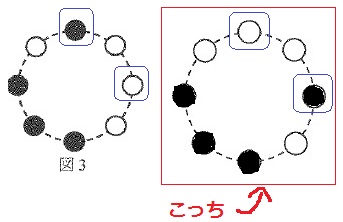
1個ずつやると面倒くさい。
そこで変わるものだけをピックアップする。
電球が点いているときは、両隣が点いているときだけ消える。
図3では右の〇だけがそうなので、それだけ消して、それ以外は点いたままにする。
電球が消えているときは、両隣が点いているときだけ点く。
図3では上の●だけがそうなので、それだけ点けて、それ以外は消えたままにする。
(2)
前問で確認した通り、両隣が点いていると変わってしまう。
→両隣が点いている状態を避ける。
〔〇〇〇〕と〇が3個以上続いたらダメ!
〔〇●〇〕と●が〇にサンドイッチしてもダメ!
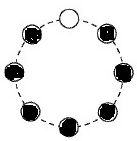
1個点くパターン。
両隣が消えている場合はセーフです。
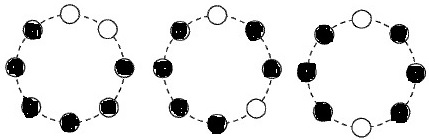
2個点くパターン。
〇〇は2個だけの連続ならばOK。
〇●〇と1個飛ばしはダメなので、〇●●〇と2個飛ばしにする。
〇●●●〇と3個飛ばしもOK。
4個飛ばしは回転させると2個飛ばしと同様なので×。
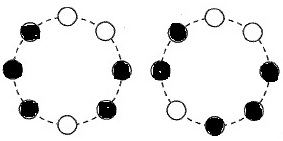
3個点くパターン。
〇は3連続できないので、1個と2個に分ける。
●が連続する固まりは左右に2個と3個で2通りできる。
問題文から『裏返し』は重複しない。
〇を1つずつ3ヶ所に配置するには、〔〇●●〕が周期的に3つ必要となり、
最低でも電球が9個以上でないとできない。

4個点くパターン。
〇は3連続以上不可なので2個と2個に分離。
5個以上はない。
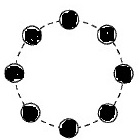
すべて点かないパターンもある。

↑答え。



コメント
(2)において、電球が全て黒の場合がありませんが、何故でしょうか?
コメントありがとうございます。
サボの見落としです(;´Д`)
修正しました。また誤りを発見された際はご一報頂けると幸いです。
サボ