問題ＰＤＦ
37名のクラスで算数のテストをしたところ、結果は下のようになりました。
70点以上が合格で、70点未満は不合格です。また得点はすべて整数です。
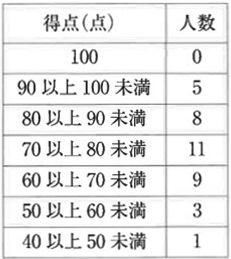
（１）
この結果から考えて、次の中から必ず正しいといえるものをすべて選びなさい。
ア：得点が一番高い人と一番低い人との差は50点以上である。
イ：得点を高い順番に並べたとき、クラスでちょうど真ん中の順番の人の得点は70点台である。
ウ：合格者の平均点は77点以上である。
エ：不合格者の平均点は65点以下である。
オ：クラスの平均点は70点より高い。
（２）
結果についてより詳しく調べてみると、さらに以下のことが分かりました。
・クラスの平均点はちょうど75点であり、不合格者の平均点はちょうど63点である。
・クラスの平均点と同じ得点の人が２人いて、クラス最高の得点の人が２人いて、
それ以外の合格者の得点はすべて異なる。
①合格者の平均点は何点ですか。
②クラスの最高点は、最も高い場合で何点ですか。
＠解説＠
（１）
必ずしも正しいとはいえない→成立しない例（反例）を１つ挙げればいい。
ア：最大値を90点、最小値を49点とすると、差は90－49＝41点×
イ：37人の中央値は（37＋１）÷２＝19番目で70～80の階級にある。〇
ウ：合格者の平均が最も低くなるパターンを想定する。
70～79は全員70点、80～89は全員80点、90～99は全員90点とする。
【70×11、80×８、90×５】
70点と90点のそれぞれ５人ずつを真ん中の80点に集める。
【70×６、80×18】
賛否はあると思いますが、ここで負の数を使います。
基準を77点とすると、70点は－７点、80点が＋３点。
－７×６＝－42点
＋３×18＝＋54点
プラスの方が大きいので、平均点は基準の77点を超える。〇
エ：不合格者の平均が最も高くなるパターンを想定する。
40～49→49点、50～59点→59点、60～69→69点
【49×１、59×３、69×９】
49点と69点から１人ずつを59点に集めて…
【59×５、69×８】
基準は65点。－６×５＝－30点、＋４×８＝＋32点
プラスが大きく、平均点は65点を超える。×
オ：平均点が最も低くなるパターンを想定する。
【40×１、50×３、60×９、70×11、80×８、90×５】
基準は70点。
－30×１＋（－20）×３＋（－10）×９＝－180点
０×11＋（＋10）×８＋（＋20）×５＝＋180点
平均点はちょうど70点。×
イ・ウ
（２）①
クラス全体の平均点75点より下の領域（青）と上の領域（赤）の面積が等しい。
？＝12×13÷24＝6.5点
合格者の平均点は、75＋6.5＝81.5点
②
合格者の合計点は、81.5×24＝1956点
70～79点の11名は、クラス平均の75点が２人いて、それ以外はすべて異なる。
⇒70～79点に１人ずつ＋75点にもう１人。
70点台の合計点は、（70＋79）×10÷２＋75＝820点
残りは、1956－820＝1136点
最高点が最も高い場合を想定するので、80点台の合計点は低く見積もる。
80点台の８人は80～87点が１人ずつとする。
（80＋87）×８÷２＝668点
残りは、1136－668＝468点
最高点の２人以外の３人は90～92点とする。
90＋91＋92＝273点
最高点２人の合計点は、468－273＝195点
195÷２＝97.5点
ということは、最高点は最も高くて97点。
（*たとえば、92点の生徒を93点にすればいい）
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント