問題PDF
兄と妹はいつも一緒に学校に歩いて通っています。ある日、兄と妹はいつもと同じ時こくにいっしょに家を出て、同じ速さで学校まで歩いていきましたが、途中で兄が忘れ物に気づき、すぐにこれまで歩いていた速さの2倍の速さで走って家に忘れ物を取りに行きました。妹は兄が忘れ物を取りに行っている間は、歩く速さをこれまでの半分にして歩きました。兄は家に帰って忘れ物を取った後すぐに家に戻ったときと同じ速さで走って妹を追いかけました。その後、学校に行く途中で兄は妹に追いついたので、二人は家を出たときと同じ速さで学校まで歩いたところ、いつもより4分遅れて学校に到着しました。
下のグラフはこの日、家を出発してから学校に到着するまでの兄と妹の様子を表しています。兄が家に戻ってから再び家を出るまでの時間は考えないものとして、次の問いに答えなさい。
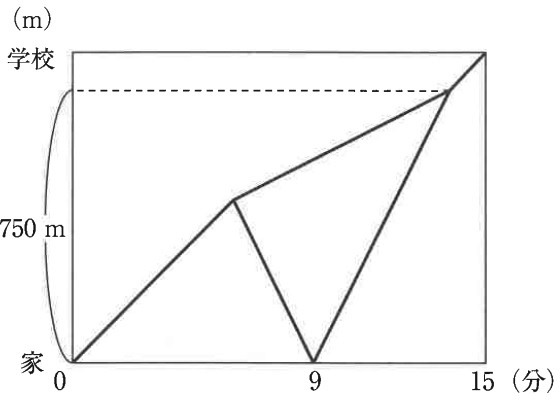
(1)
兄が忘れ物に気づいたのは、出発してから何分後ですか。
(2)
兄が家で忘れ物を取った後、妹に追いついたのは出発してから何分後ですか。
(3)
家から学校までの道のりは何mですか。
@解説@
(1)
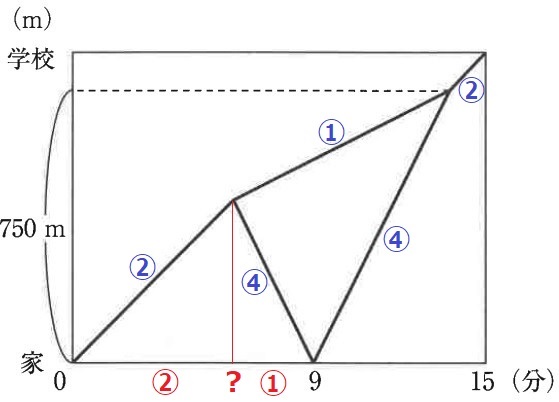
まず、速さの比を整理しておく。
最も遅い妹の速さを①とすると、2人のときは②、兄は④の速さ。
兄が忘れ物に気がついた地点から家までの距離において、
速さの比は2人:兄=1:2だから、時間は逆比で②:①
③=9分なので、9×②/③=6分後
(2)
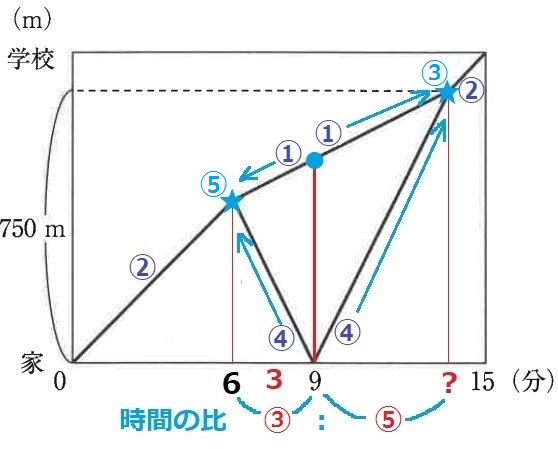
兄が家に戻った9分後を基準に考える。
9分後の状態から逆再生すると、妹は①、兄は④で近づくから速さの和は⑤
9分後から時を進めると、同じ距離を兄が妹を追いかけるから、速さの差は④-①=③
速さの比が⑤:③→時間は逆比で③:⑤
③=3分なので、⑤=5分
9+5=14分後
(3)
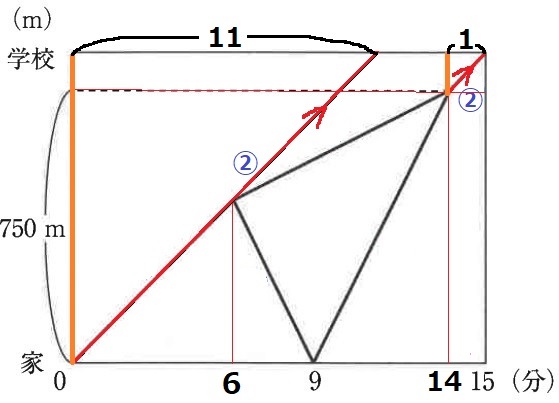
750mを使うので、14分後の位置がポイントになる。
14分後から学校までは速さ②で1分。
一方で、忘れ物のトラブルがなければ、速さ②のままで15-4=11分で着いた。
最初の線をうえまで延長させると、11分後に学校へ到着する。
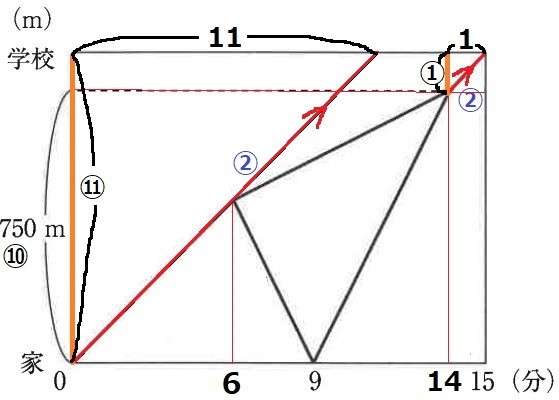
速さが一定→時間と距離は比例。
家~学校の距離を⑪とすると、14~15分後の距離は①
残りの⑩が750mにあたる。
家~学校までの距離は、750×⑪/⑩=825m



コメント