問題PDF
下の図の(あ)と(い)の三角形は角の大きさがそれぞれ異なるため、同じ形の三角形ではありません。しかし、図のように三角形の内部に直線をかいて三角形を分割すると、(う)と(え)の三角形は角の大きさがそれぞれ40°、50°、90°である同じ形の三角形に、(お)と(か)の三角形は角の大きさがそれぞれ30°、60°、90°である同じ形の三角形になり、2組の同じ形の三角形に分割することができます。
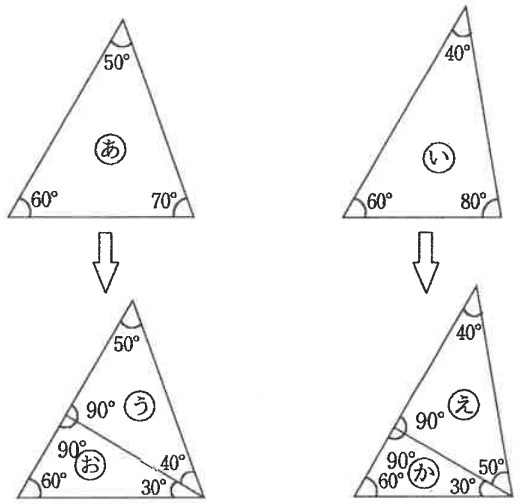
(1)
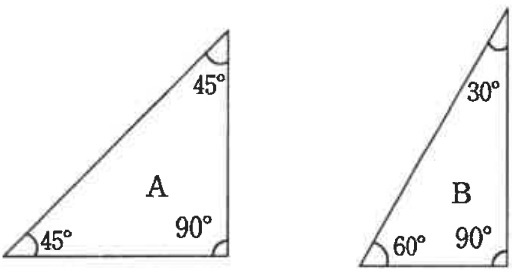
Aの三角形とBの三角形の内部に直線を1本ずつかいて、2組の同じ形の三角形に分割しなさい。
解答らんには、上の図のように分割した三角形の角度をすべて記入すること。

(2)
Aの三角形とBの三角形の内部に直線を2本ずつかいて、3組の同じ形の三角形に分割しなさい。
解答らんには、上の図のように分割した三角形の角度をすべて記入すること。

(3)
(あ)の三角形と(い)の三角形の内部に点を1点をとり、その点と各頂点を結ぶことで、
3組の同じ形の三角形に分割しなさい。解答らんには、上の図のように分割した三角形の
角度をすべて記入すること。ただし、三角形の内部に、辺はふくみません。

@解説@
(1)
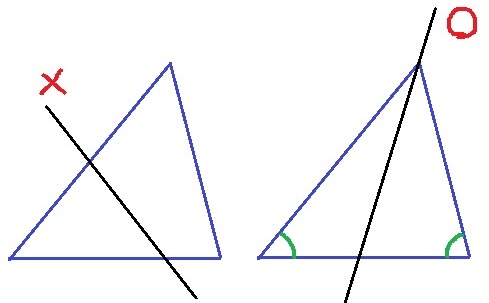
中途半端なところで分割すると、一方が四角形になってしまうので不適。
必ず直線は3つの頂点のどれかを通過する。
1つの内角が分割され、2つの内角は生き残ることになる。
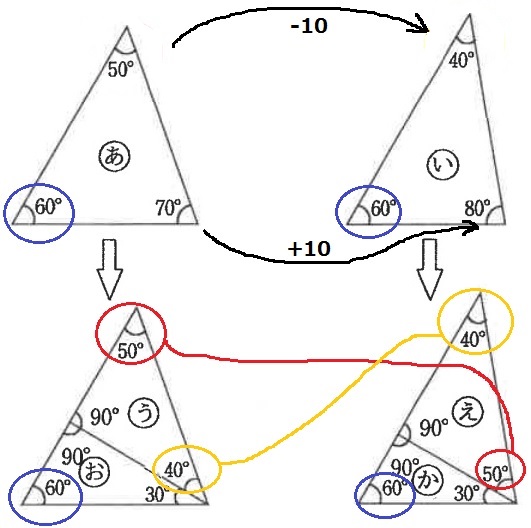
内角を観察すると、(あ)と(い)は60°が同じで、50°→40°、70°→80°は±10°
最も大きい(あ)の70°と(い)の80°を分割し、
50°と40°を交換するように(う)と(え)で分ける。
すると、下が30°―60°―90°の内角で等しくなる。
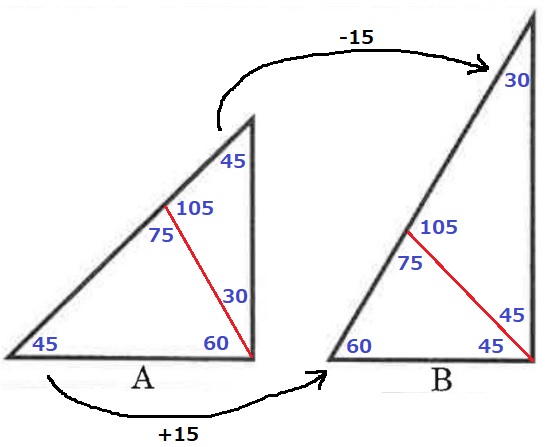
最も大きい内角である直角を分割する。
45°→30°、45°→60°は±15°
45°と30°、45°と60°を交換するような形で分割する。
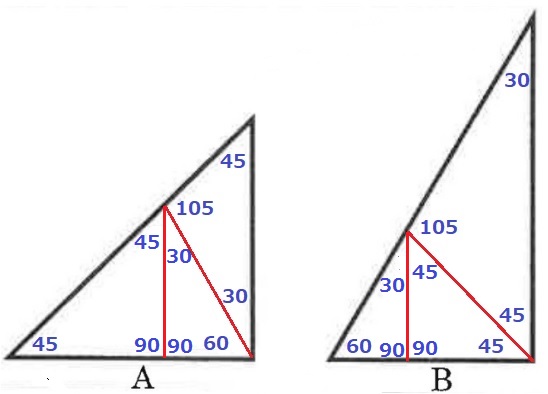
(2)

前問の答えを活用する。
右側の三角形は同じ形(相似)を上下反対にしたものなので、
上図のように分割すれば題意に適する。
@@
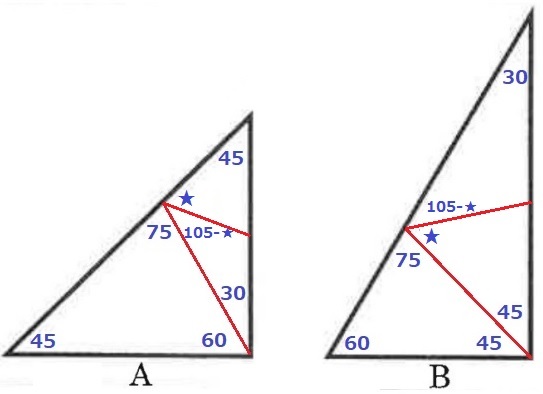
★は何度でもいいので、解答は無数にある。
もちろん、下の三角形を左右に分割してもOK。

このように分割してもいけました。
(3)

三角形の内部に点をとり、3組の同じ形の三角形で分割する。
外側の底角の組み合わせさえ確定すれば、中の方はあとで処理できる。
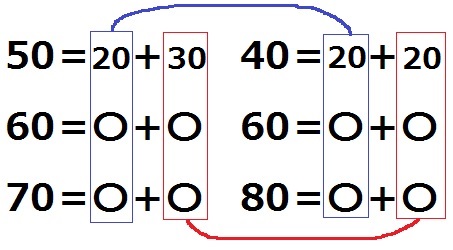
一方の項と他方の項の組み合わせが同じになればいい。
50と40、70と80が±10°差。
50と40では青枠を20にして、赤枠に30・20を配置。
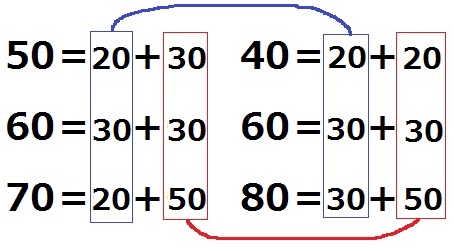
70と80の赤枠に50、青枠に20・30を配置。
60はすべて30。

三角形は2種類だが、3組の同じ形に分割しているので大丈夫なはず。
@@

こちらも解答は複数ある。



コメント