2019年度　サレジオ学院中学過去問【算数】大問２解説

問題ＰＤＦ
次の〔　　〕にあてはまる数を答えなさい。
（１）
200、329、415をそれぞれ２以上の同じ整数〔　ア　〕で割ると、
余りはすべて同じ〔　イ　〕になります。

（２）
川上のＡ地点と川下のＢ地点を結ぶ船があり、上りにかかる時間が下りにかかる時間のちょうど２倍になるのは、船自体の速さが川の流れの速さの〔　　〕倍のときです。
ただし、川の流れの速さも、船自体の速さも一定であるとします。

（３）
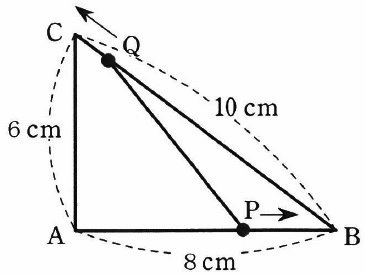
下図のような三角形ＡＢＣがあります。
点Ｐは毎秒２ｃｍの速さでＡ→Ｂ→Ｃ→Ａ、点Ｑは毎秒３ｃｍの速さでＢ→Ｃ→Ａ→Ｂの順に、それぞれ三角形ＡＢＣの辺上を１周だけ動きます。点Ｐと点Ｑが、それぞれ点Ａ、点Ｂを同時に出発すると、〔　　〕秒後に辺ＰＱと辺ＢＣが平行になります。

（４）
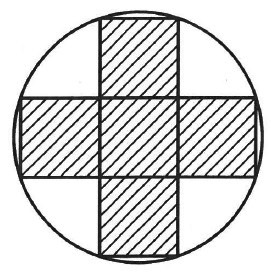
下図のように、同じ大きさの５つの正方形が重なることなく
半径が６ｃｍの円の内側にくっついています。
このとき、斜線部分の面積は〔　　〕ｃｍ²です。

（５）
〔図１〕のような直方体の形をした水そうの中に、深さが４ｃｍとなるように水が入っています。〔図２〕のような三角柱の形をした物体を、〔図２〕の向きのまま水そうの底に沈めると、水面が２ｃｍ上昇します。このとき、水の体積は〔　　〕ｃｍ³です。

（２）
流水算の基礎。
速さの比は時間の逆比なので、上りの速さ：下りの速さ＝１：２
速さで線分図。

上り＝静水時－川の流れ、下り＝静水時＋川の流れ
川の流れ＝①とおくと、静水時の船の速さ＝③となる→３倍。

（３）
ＢＣ//ＰＱとなる図を描いてみよう。

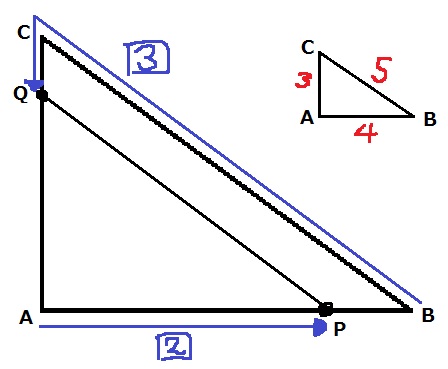
ＰとＱの速さが２：３なので、進んだ距離も２：３となる。
△ＡＰＱに注目！
平行線から２角が等しく、△ＡＢＣ∽△ＡＰＱ。
△ＡＰＱの辺の比は、10：８：６＝５：４：３となる。

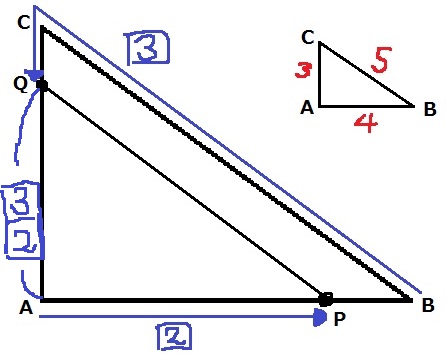
ＡＱ＝□２×３/４＝□３/２
ＡＣ＋ＣＢ＝□３/２＋□３＝□９/２＝16ｃｍ
ＡＰ＝16×２/ 9/2＝64/９ｃｍ

Ｐは毎秒２ｃｍ動くので、64/９÷２＝32/９秒後

（４）
変形ですな(´ω`).。0
半径がわかっているので、円の中心から半径や直径を伸ばしてみる。

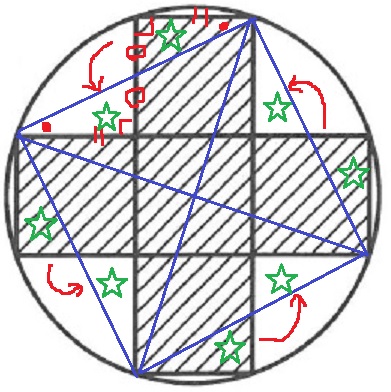
一辺両端角が等しい→合同の直角三角形が４箇所ある。
これを中に収めると、対角線が円の直径（12ｃｍ）に相当する正方形になる。
12×12÷２＝72ｃｍ²

（５）
三角柱を沈めたとき、三角柱が押しのけた水の体積は水深４ｃｍまで。

三角柱の奥行きは５ｃｍ。
水に浸かる部分は、（４＋８）×４÷２×５＝120ｃｍ³

問題は、うえの２ｃｍの部分が水位の上昇に影響する。
その体積は、（２＋４）×２÷２×５＝30ｃｍ³
押しのけられた水の体積120ｃｍ³＝水位が上昇した２ｃｍ分の水槽の体積－三角柱の一部30ｃｍ³
水位が上昇した２ｃｍ分の水槽の体積＝120＋30＝150ｃｍ³
水槽２ｃｍが150ｃｍ³。
最初の水深は４ｃｍなので、水の体積は300ｃｍ³。
難関中（算数科）解説ページに戻る