問題PDF
(1)

(2)
白色、黄色、赤色のさいころがそれぞれ1個ずつあります。
この3個のさいころを同時に投げます。
①どの2個のさいころの出る目の差も4以下となるような、目の出方は何通りですか。
②出る目のもっとも大きい目が5であるような、目の出方は何通りですか。
(3)
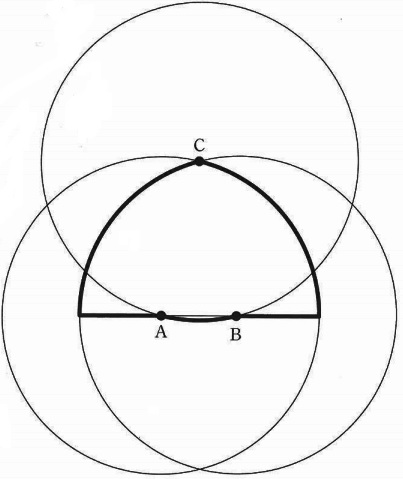
図の3つの円はどれも半径が4cmで、それぞれの中心は点A、B、Cです。
点A、Bを中心とする円は、どちらも点Cを通り、直線ABの長さは2cmです。
図の太線の長さは何cmですか。
(4)

①ウにあてはまる整数を求めなさい。
②ア、イにあてはまる整数をそれぞれ求めなさい。
(5)
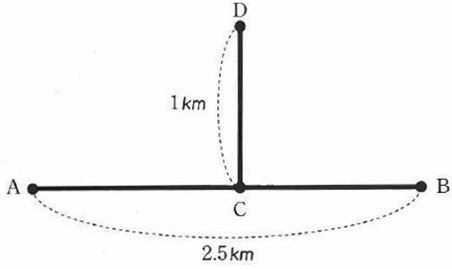
A、B、C、Dの4人の家は、図のように2本の直線道路でつながっています。
Aさんは自分の家からCさんの家まで分速150mの速さで移動し、
すぐにDさんの家まで分速90mの速さで移動しました。
Bさんは、自分の家からCさんの家まで分速90mの速さで移動し、
すぐにDさんの家まで分速150mの速さで移動しました。
AさんとBさんは同時に自分の家を出発し、同時にDさんの家に着きました。
AさんとCさんの家は何mはなれていますか。
@解説@
(1)

計算するだけだが、とちる危険が怖い(;’∀’)
1.75=7/4
答えは21/13。
(2)①
『どの2個のさいころの出る目の差も4以下』
→3つのサイコロのうち、どの2つをとっても差が1~4。
出目の差は最大で6-1=5だから、【全体-出目の差5】を計算した方が早い(余事象)。
出目の差5⇒3つのうち1つは〔1〕、残りの1つは〔6〕
〔1・6・それ以外〕か〔1・6・1or6〕の組み合わせを考える。
■〔1と6とそれ以外〕
1・6・□(□は2~5)
□は2~5で4通り。
順番は、3×2×1=6通り
よって、4×6=24通り
■〔1と6のみ〕
1・1・6 →3通り
1・6・6 →3通り
計6通り
余事象の合計は、24+6=30通り
全体は、6×6×6=216通り
216-30=186通り
②
『出目の最大が5』
5の数で場合分け。
■5が1つ→5、□、□
□=1~4で4通り。順番の入れ替えは3通り。
4×4×3=48通り
■5が2つ→5、5、□
4×3=12通り
■5が3つ→5、5、5
1通り
48+12+1=61通り
(3)

△ABCをつくる。
それぞれの角度は何度かわからないが、合計は三角形の内角の和である180°
これらの角を中心とする扇形の弧は赤い部分となる。
これにABの左右にある直線部分、(4-2)×2=4cmを足す。
4×2×3.14×180/360+4=16.56cm
(4)①
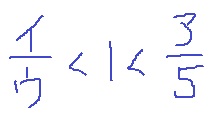
不等式で示すとこうなる。
ア/5-イ/ウ=1/3だから、分母の5と3の最小公倍数15で通分してみる。

1/3=5/15で、ア×3-イ×〇=5
ア×3の積が15の次の16だとすると、イ×〇は11となる。
11≦イ×〇≦14
ウ×〇=15なので、(ウ、〇)の組み合わせは、
(1、15)(15、1)(3、5)(5、3)
ウが1だと分母が1となり、イ/ウは1を超すので×。
11≦イ×〇≦14で、このなかに5の倍数がないから、〇=5もなし。
(ウ、〇)=(15、1)or(5、3)
仮に(5、3)だと、イ×〇=3の倍数だから、11~14の中では12となる。
すると、ア×3=12+5=17となり、アが3で割り切れず、整数にならない。
よって、(ウ、〇)=(15、1)
ウ=15
②
〇=1より、11≦イ≦14
これに+5をして、16≦ア×3≦19
3の倍数は18しかない。
ア×3=18 ア=6
イ=18-5=13
(5)
C-D間(1000m)をAは分速90m、Bは分速150mで移動する。
AはBよりも、1000/90-1000/150=40/9分かかる。
スタートとゴールは同じ時間なので、
A-C間の時間よりB-C間の時間が40/9分多くかかるようにすればいい。
ここで鶴亀算の面積図を利用。
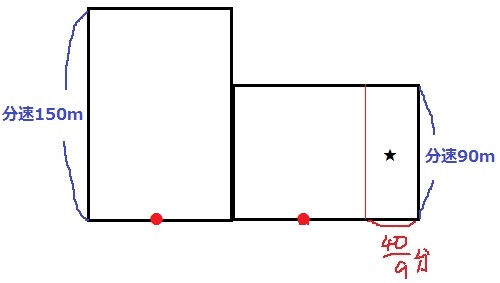
横は時間、縦が速さ、面積が距離。
2つの長方形の面積の合計は、A-B間の2500m。
右の長方形の横は、左の長方形よりも40/9長い。
★の面積…90×40/9=400m
★を除いた面積…2500-400=2100m
★を除いた2つの長方形は横●が等しいので、
●に合わせて2つの長方形を縦に重ねると、●×(90+150)=2100m
●=2100/240=70/8分
よって、A-C間(左の長方形)は、150×70/8=10500/8=1312.5m
@@@@
中1レベルの1次方程式を使えばもっと楽。
A-C間の距離をxmとおくと、B-C間は2500-x
x/150+1000/90=(2500-x)/90+1000/150
これを解いて、x=1312.5



コメント