問題PDF
クラス対抗の球技会が行われます。
バスケットボール、ドッジボール、サッカー、卓球の4つの競技で、
1人1つまたは2つの競技に出場します。
あるクラスの生徒の出場は次の通りです。
(ア)サッカーと卓球の両方に出場する生徒はいません。
(イ)2つに出場する生徒は、9人です。
(ウ)バスケットボールとドッジボールの両方に出場する人数は、
バスケットボールに出場する人数の1/5、
ドッジボールに出場する人数の1/4です。
(エ)バスケットボールに出場しない生徒は、20人です。
(オ)バスケットボール、サッカー、卓球のうち、2つに出場する生徒は、
ドッジボールのみに出場する生徒より3人少ないです。
(1)バスケットボールとドッジボールの両方に出場する生徒は何人ですか。
(2)サッカーまたは卓球に出場する生徒は何人ですか。
(3)このクラスの人数は何人ですか。
@解説@
情報整理がとにかく難しくてイヤになる!
2つ重複して出場する者が9人いるが、配分がわからない。
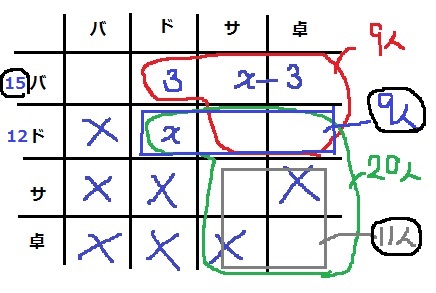
要素が4つあるので、ベン図ではなく表で処理する。
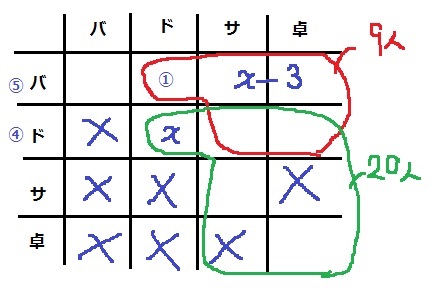
見るべきマスを少なくするために、重複する左下6つを×。
(ア)【サ・卓】のマスを×。
(イ)対角線の斜め4マスが1つの競技のみ。2つ参加する人は赤い枠9人。
(ウ)バを⑤、ドを④とおくと、【バ・ド】が①
(エ)バ行以外の緑の枠が20人。
(オ)ドッジボールのみ【ド・ド】をxとおく。
バ、サ、卓で2つ出る人は【バ・サ】と【バ・卓】のところは、x-3となる。
(1)
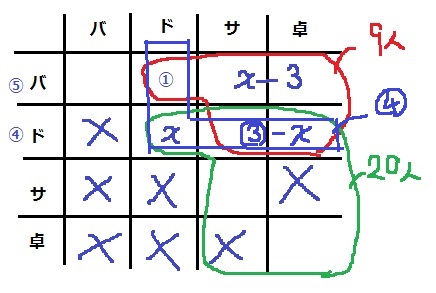
この表の弱点ですが、ドの④はL字になります。
重複を避けるために【ド・バ】を消したので、【バ・ド】を見るからです。
【ド・サ】と【ド・卓】の和は、④-①-x=③-x
赤枠に注目。
①+(x-3)+(③-x)=9
④=12
①=3
バスケットボールとドッジボールの両方に出場する生徒は3人。
*xの値がわからなくても、xを消せる等式を探す。
20人より9人のマスに情報が偏っているので、=9の等式を作る。
(2)
サッカーと卓球は右2列。
前問より、【バ・ド】は3人、バは15人、ドは12人とわかる。
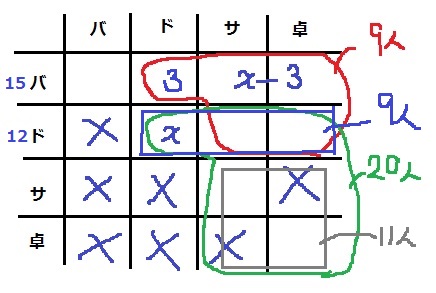
2行目の和を求める。
ド-【バ・ド】=【ド・ド】+【ド・サ】+【ド・卓】=12-3=9人
緑枠より、下の【サ・サ】と【卓・卓】の和は、20-9=11人
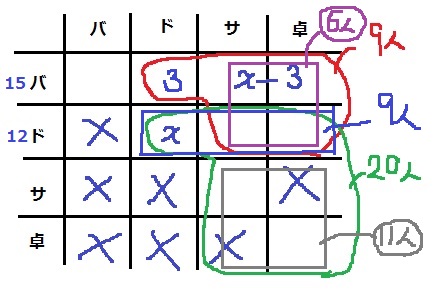
その上の4マス【バ・サ】【バ・卓】【ド・サ】【ド・卓】の和は、
9(赤枠)-3=6人
したがって、サッカーまたは卓球に出場する生徒は、
6+11=17人
(3)
クラスの合計は○で囲ったところ。
15+9+11=35人
*xの値やその他の空欄がわからなくても、すべて出せてしまう。
が、情報整理と表のどこを見るべきかで、思考が迷宮入りしやすい…。
最後の大問で一体どれほどの生徒が正解できたのだろうか。



コメント