2021年度　豊島岡女子学園中学３回目過去問【算数】大問４解説

問題ＰＤＦ
下の図のように、ある規則にしたがって整数がマスの中に１つずつ書かれています。

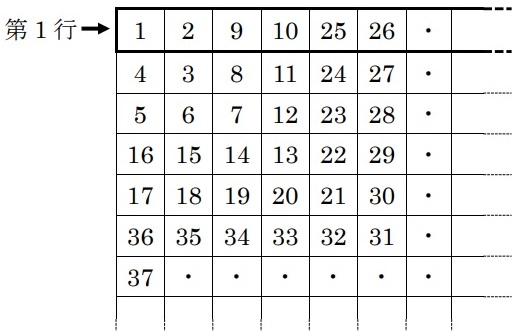
第１行の数を１つ選びＡとします。
Ａの１つ右のマスに書かれた数をＢとし、Ａの１つ下のマスに書かれた数をＣとし、
Ｃの１つ右のマスに書かれた数をＤとして、４つの数Ａ、Ｂ、Ｃ、Ｄの和をＸとします。
例えば、Ａ＝９のときはＸ＝９＋10＋８＋11＝38であり、
Ａ＝10のときはＸ＝10＋25＋11＋24＝70です。
このとき、次の各問いに答えなさい。

（１）
Ａ＝122のとき、Ｘはいくつですか。

（２）
Ｘ＝2710のとき、Ａはいくつですか。

＠解説＠
（１）

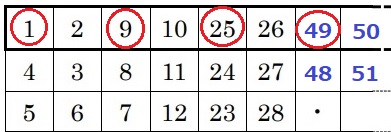
１行目にある特徴的な数といえば、奇数の平方根。
１行目の奇数番目は奇数×奇数、次の偶数番目は＋１

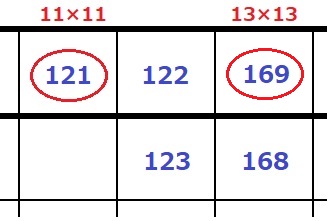
Ｘ＝122＋123＋168＋169＝582

（２）
左上のＡが奇数の平方数であるか否かの２択。

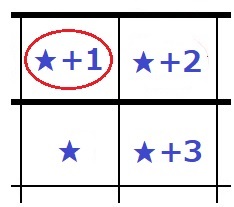
Ａが奇数の平方数である場合、Ａ～Ｄは連続する４つの整数。
最も小さいＣを★とすると、
Ｘ＝★＋（★＋１）＋（★＋２）＋（★＋３）
＝★×４＋６＝2710
★×４＝2704
★＝676

Ａ＝★＋１＝677だが、25×25＝625なので奇数の平方数ではない！
ということは、Ａは676に近い奇数の平方数である625に＋１をした626である。

＠検算＠
Ａ＝626、Ｂ＝27×27＝729、Ｃ＝627、Ｄ＝728
Ｘ＝626＋729＋627＋728＝2710