（１）
下の図は、文字盤のない時計を長針が真上にくるようにおいたものです。
このとき、（あ）と（え）の角の大きさの比は１：２、
（い）と（う）の角の大きさの比は３：１となりました。
次の①、②に答えなさい。
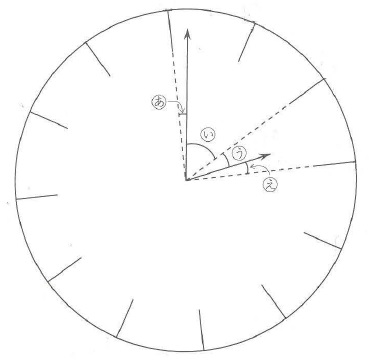
①（う）の角度を求めなさい。求め方も書きなさい。
②この時計は何時何分を表していますか。
（２）
分子と分母の和が２、４、６、８、10…となるような分数を、
約分できる分数でも約分せずに次のように並べていきます。
次の①、②に答えなさい。
①左から数えて50番目の分数を求めなさい。
②３/25は左から数えて何番目の分数ですか。
＠解説＠
（１）①
文字盤の１つの目盛りは30°。
①＋□３＝60°、②＋□１＝30°の関係が成り立つ。
後半の式を２倍して60°に統一すると、①＋□３＝④＋□２と等式ができる。
式を整理すると、□１＝③
（算数の世界で移項が嫌いであれば、両辺から①と□２を除外すると説明）
（う）＋（え）＝③＋②＝⑤（＝30°）
（う）…30°×③/⑤＝18°
②
１分間あたり、短針は30°÷60分＝0.5°進む。
長針が12時から図の位置まで動いたあいだに短針は18°進んだので、
18÷0.5＝36分
長針は７と８にあり、短針は９と10の間にある。
９時36分
（２）①
このように区切ると、項の数が〔１・３・５…〕と奇数個で増えていく。
50に近いところまで足していく。
〇番目までの奇数の和は、〇×〇と平方数で計算できる！
奇数の数列で13は７番目なので、１～13までの奇数の和は７×７＝49
グループの１番はじめの分数の分母も〔１・３・５…〕だから、
50番目の分数は分母が15、分子が１→１/15
②
分子が３なので、３/25を含むグループの１番はじめの分数は、３/25→２/26→１/27。
（分子分母の和は28）
奇数の数列のなかで、27の手前にある25は（25＋１）÷２＝13番目
１～25までの奇数の和は、13×13＝169
分母が25のグループの最後が169番目。
そこから３番目が３/27だから、172番目となる。
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント