問題PDF
(1)
次の展開図で点線部分を折り目としてできる立体の体積を求めなさい。

(2)
分子が1で分母が整数である分数を単位分数といいます。
ここで、分子が1でない分数を分母の異なる単位分数の和として表すことを考えます。
たとえば、3/5=1/2+1/10や、4/9=1/3+1/9です。
次の各問いに答えなさい。
①次の手順で、5/11を単位分数の和として表しました。
ア~カには整数が入ります。オ、カに入る整数を答えなさい。

②①と同じ手順で、3/7を単位分数の和として表しなさい。求め方も書きなさい。
@解説@
(1)
まずは立体図形を描く。
側面は底面に対して垂直なので、左の直角三角形を底面にもってくる。
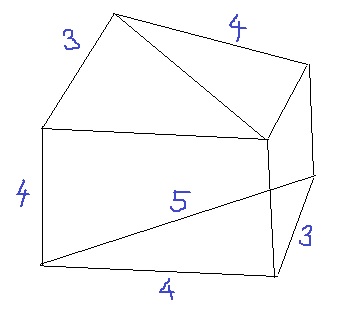
背面に五角形。天井が屋根のようになる。
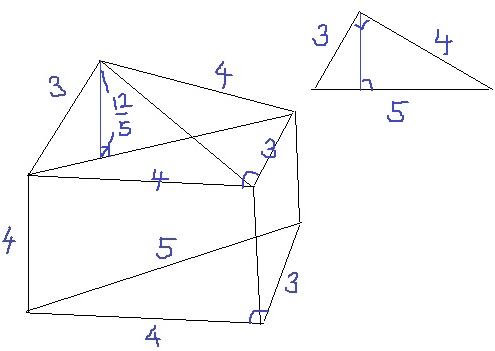
下の三角柱、上の三角錐に分ける。
三角錐の高さは3:4:5の直角三角形において、底辺を5とおいたときの高さに等しい。
3×4÷5=12/5cm
3×4÷2×4+3×4÷2×12/5÷3
=24+4.8=28.8cm3
(2)①

5/11を単位分数の和で表す。
〔1〕分子÷分母をする。1/(商+1)<5/11<1/(商)
〔2〕5/11-1/3=4/33
〔3〕〔1〕と同様。33÷4=8…1
1/9<4/33<1/8
〔4〕4/33-1/9=1/99
オ…9、カ…99
@@
どうしてこうなるのだろう?
5/11は、1を11で割ったうちの5。
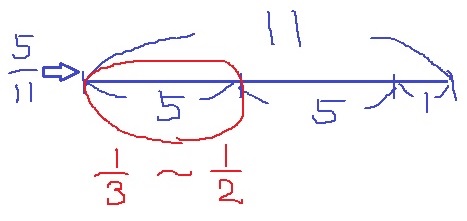
分子を分母で割り、商が2で余りがでる。
⇒5は11の半分より下⇒5/11を単位分数の範囲で示すと1/2より下、1/3より上。

分子の5のうち、最大の単位分数である1/3をひく。
残りの4/33で同様の作業をしていく。
[1]割り算で分数の中から最大の単位分数を探す。
[2]最大の単位分数をひいて、残りから再度、最大の単位分数を探す…
[3]最後が単位分数になったら、すべてを足す。
②
手順を模倣すればOK。
7÷3=2…1 1/3<3/7<1/2
3/7-1/3=2/21
21÷2=10…1 1/11<2/21<1/10
2/21-1/11=1/231 ←分子が1なので終了
3/7=1/3+1/11+1/231



コメント