問題PDF
図1のように点P、Qは円Oの円周上の点Aから同時に出発し、
それぞれ一定の速さで円周上を以下のように動きます。
①Qの方がPよりも速く動く。
②Pは常に時計回りに動く。
③Qは始めは反時計回りに動くが、Pと重なるたびに向きを変えて動く。
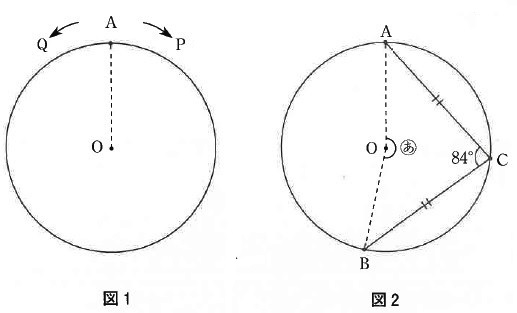
図2の点BはPとQが重なった2回目に重なった点であり、
点CはPとQが5回目に重なった点です。このとき、AC=BCとなりました。
ただし、2回目に重なったのはPが円Oを1周する前であり、
5回目に重なったのはPが点Aを1回だけ通った後でした。
次の各問いに答えなさい。
(1)
PとQが2回目に重なるまでにPが点Aから進んだときの角度(あ)を求めなさい。
(2)
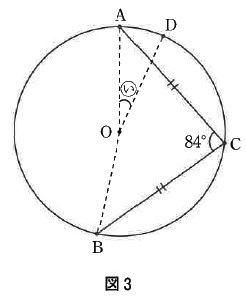
PとQが4回目に重なったのは図3の点Dでした。角度(い)を求めなさい。
(3)
QはPの何倍の速さで動いていますか。
(4)
PとQが200回重なるまでに何回点A上で重なりますか。
@解説@
(1)
図2の平面図形から考える。

補助線をひくと2つの二等辺が見つかる。
●●=84°
四角形AOBCで、(あ)=360-84×2(●●●●)=192°
(2)
左の∠AOB=360-192=168°
ここで速さを考える。
Pは常に時計回り。
Qは反時計回りだが、Pと会うと時計回りに変わる。
1回目の重なりまで、PとQはAから違う方向で出発する。
1回目の重なりでQはPと同じ方向に変え、Pを周回遅れにして2回目に重なる。
つまり、奇数回ではPとQは異なる方向に向かい出会う形となるが、
偶数回ではPとQが同じ方向となり、QがPを追いつく形で重なる。
ということは、Aから出発~2回目の重なり(B)までと、
2回目の重なり(B)~4回目の重なり(D)までの時間が同じ。
Pが進んだA~B間とB~D間の距離も同じ。
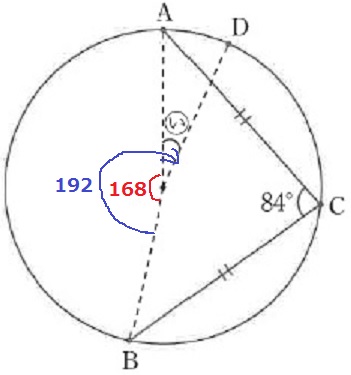
∠BOD=192°
(い)=192-168=24°
(3)
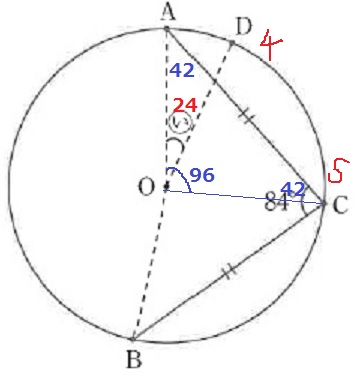
△AOCで、∠AOC=180-42×2=96°
前問から∠AOD=24°なので、
4回目~5回目の重なりまでPが移動した距離は、96-24=72°
同じ時間をQは、360-72=288°動く。
速さの比は、P:Q=72:288=1:4
したがって、QはPの4倍の速さで動いている。
(4)
Pの進む距離に注目。
前問から、PはAからスタートして72度の場所でQに会う(1回目の重なり)。
2回目は(1)の角度あ=192°だったので、
Pが192-72=120°進んでから、Qに追いつかれる。
以下、Pの進む距離は+72、+120が交互に繰り返される。
0、72、192、264、384・・
72°は5分の1周、120°は3分の1周なので、
一周を【15】とおき、+【3】、+【5】の数列、
【3】、【8】、【11】、【16】、【19】…で、【15】の倍数の個数を考える。
コツは〔8の倍数〕と〔8の倍数-5〕で2つのグループに分けること。
〔8の倍数〕は100個ある。
そのうち、15の倍数は、100÷15=6…5→6個
〔8の倍数-5〕も100個ある。
最後の数は、100×8-5=795
【3】、【11】、【19】、【27】…【795】
調べていくと、【75】(=15×5)で初めて15の倍数となる。
次は、15×(5+8)、15×(5+16)、15×(5+24)…15×(5+48)
795=15×53=15×(5+48)なので終了→計7個
したがって、7+6=13個



コメント