問題PDF
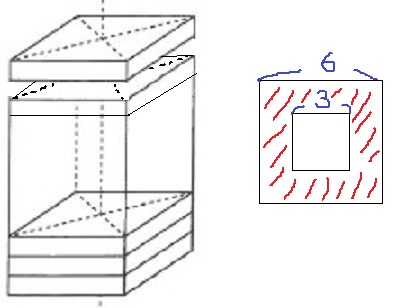
底面が1辺3cmの正方形で高さが1cmの直方体Aと、底面が1辺6cmの正方形で高さが1cmの直方体Bが、それぞれ12個ずつあります。これら24個の直方体のうち12個を積み重ねて立体を作ります。下の図1は直方体Aだけを12個積み重ねて作ったものであり、図2は直方体Bだけを12個積み重ねて作ったものです。このように、同じ直方体を重ねるときは、上の直方体の底面と下の直方体の底面がぴったり合うように重ねます。また、違う直方体を重ねるときは、図3のように、上の直方体と下の直方体の底面の真ん中の点がぴったり合うように重ねます。

表面全体の面積がもっとも大きい立体を作ることにします。
このとき、次の( ア )~( オ )にあてはまる数を答えなさい。
ただし、立体の表面全体の面積を求めるときには、立体の下側の面積も考えるものとします。
まず、図2の立体を作ります。この立体の表面全体の面積は( ア )cm2です。次に、使われている直方体Bを直方体Aにかえていきます。図2の立体の一番上の直方体Bの1個だけを直方体Aにかえるとすると、表面全体の面積は( イ )cm2となり、図2の立体の上から2番目の直方体Bの1個だけを直方体Aにかえるとすると、表面全体の面積は( ウ )cm2となります。表面全体の面積がもっとも大きい立体は、図2の立体の直方体Bを( エ )個だけ直方体Aにかえて作ることができ、そのときの立体の表面全体の面積は( オ )cm2です。
@解説@
方針は立てやすい。計算ミスに注意!

ア…左の直方体の表面積。
6×6×2+6×12×4=360cm2
イ…一番上だけをAに変える。
天井の面積は変わらない(赤色の和)
側面積は、1×6×4-1×3×4=12cm2減る。
360-12=348cm2
ウ…2段目だけをAに変える。
中の上下で、(6×6-3×3)×2=54cm2増える。
側面積は先ほどと同様、12cm2減るので、全体では54-12=42cm2増える。
360+42=402cm2
エ…一番上と下をAに変えてしまうと、イのように表面積が減ってしまう。
間はAとBを互い違いにする。
〔B・A・B・A・B・A・B・A・B・A・B・B〕
5枚のBをAに変える。
オ…B1枚をAに変えると、ウより42cm2増える。
5枚変えるので、360+42×5=570cm2



コメント