2019年度　大阪府公立高校過去問【数学】Ａ問題解説

平均64.2点
問題はコチラ→ＰＤＦファイル
2019年度大阪府Ｂ問題・Ｃ問題は別ページ。

大問１（計算）

（１）　75.0％
２－（－５）
＝２＋５＝７

（２）　68.0％
－９×４/３＝－12

（３）　65.0％
13－４²
＝13－16＝－３

（４）　45.0％
３ｘ＋７＋３（ｘ－２）
＝３ｘ＋７＋３ｘ－６
＝６ｘ＋１

（５）　53.0％
４ｘ²×２ｘ
＝８ｘ³

（６）　55.0％
√50－３√２
＝５√２－３√２
＝２√２

大問２（小問集合）

（１）　63.0％
６ａ－４
＝６×２－４＝８

（２）　44.0％
配った枚数は９ｘなので、９ｘ＞50→イ

（３）　63.0％
ｘ＝５×６/３＝10

（４）　26.0％！
最頻値（モード）は一番表れている数字→55

（５）　41.3％
加減法がやりやすいかな。
上の式と下の式を足すとｙが消え、４ｘ＝16
ｘ＝４
ｙ＝－１

（６）　39.0％
表を○、裏を●とすると、
○○、○●、●○、●●のいずれか。
１/４

（７）　26.3％！
ｘ²＋９ｘ＋14
＝（ｘ＋２）（ｘ＋７）＝０
ｘ＝－２、－７

（８）　35.0％
傾きａが正なので、グラフは右上となる。
切片ｂが正なので、ｙ軸との交点も正→ア

（９）　23.0％！
５＝（－３）²ａ
９ａ＝５
ａ＝５/９

（10）①78.0％　②14.0％！
①円錐の投影図→エ
②４×４×π×６×１/３＝32πｃｍ³
ここまでで５１点。

大問３（数量変化）

（１）ア…75.0％　イ…66.0％
イスを１個増やすと90ｃｍ伸びる。
＋90をして、40、130、220、310、400、490、580…
ア…310、イ…580

（２）　17.4％！
文字を使って一般式を書く。
初めは40、90ずつ足される。
90は（ｘ－１）個であることに注意！
ｙ＝40＋90（ｘ－１）
ｙ＝90ｘ－50

（３）　33.0％
前問の式に、ｙ＝1660を代入
90ｘ－50＝1660
ｘ＝19

大問4（平面図形）

（１）　15.0％！
△ＡＢＣは１：１：√２の直角二等辺。
ＡＢ＝３ｃｍなので、ＡＣ＝３×√２/１=３√２ｃｍ

（２）　11.3％！
ＣＥ＝ｘ、ＣＤ＝３
ｘ×３÷２＝３/２cm²

（３）ａ…63.0％　ｂ…59.3％　ｃ…51.0％
相似の証明。
誘導に従って空欄を埋める。

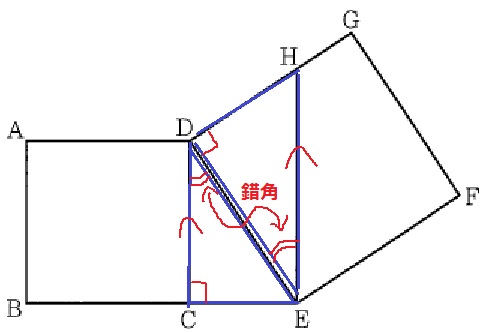
正方形の１つの内角＋錯角⇒２角が等しい。
角度は対応する順にアルファベットを書くこと！
ａ：ＥＤＨ　ｂ：ＤＥＨ　ｃ：ウ

（４）　4.1％!!
説明記述。書き方は公式解答を参照。
ＣＤ＝３、ＣＥ＝２
△ＤＣＥで三平方。
ＤＥ＝√13
前問で、△ＤＣＥ∽△ＥＤＨを証明したので、これを使う。
ＣＥ：ＤＨ＝ＣＤ：ＤＥ＝３：√13
ＤＨ＝√13×２/３＝２√13/３ｃｍ
公立高校入試解説ページに戻る