平均58.0点
問題はこちら→東進ハイスクールさん(解答)
2019年大阪A問題・2019年大阪B問題は別ページ。
大問1(小問集合)
(1) 87.3%
x2-10x+2
=x(x-10)+2
=(5-2√3)(-5-2√3)+2
=-(5-2√3)(5+2√3)+2 ←マイナスを外に出して和と差の平方にする
=-{52-(2√3)2}+2
=-(25-12)+2
=-11
(2) 87.7%
x-y+1=3x+7 ⇒-2x-y=6
3x+7=-2y ⇒3x+2y=-7
x-y+1=-2y ⇒x+y=-1
いずれから2つを選んで連立を組む。
x=-5、y=4
(3) 83.6%
(a+2b)2+a+2b-2
=(a+2b)2+(a+2b)-2 ←(a+2b)をXと置く
=X2+X-2
=(X+2)(X-1) ←Xを(a+2b)に戻す
=(a+2b+2)(a+2b-1)
(4) 90.9%
全てを2乗する。
(√31)2=31、(8/√2)2=64/2=32、5.52=30.25
5.5<√31<8/√2→オ
(5) 58.2%
素数は1を含まない。2、3、5、7、11…
2a/bに当てはめて、(a、b)の組み合わせを探す。
■2
(1、1)(2、2)(3、3)(4、4)(5、5)(6、6)
■3
(2、3)(4、6)
■5
(2、5)
計9通り
9/36=1/4
(6) 20.9%!
ランダムで40個取り出したとき、初めは黒:白=32:8=4:1であったが、
白100個を追加して同様に繰りかえすと、黒:白=28:12=7:3となった。
黒の数が変わっていないことに注目。黒を通分してみる。

白の増加分、□5が100個に相当する。
黒の数は、100×28/5=560個
(7) 50.9%
a=2n-1、b=2n+1とおく(nは自然数)
b2-a2
=(b+a)(b-a)
=(2n+1+2n-1)(2n+1-2n+1)
=4n×2=8n
これが100の倍数となるので、8n=100kとおいてみる。
試しに、k=1をいれるとnが自然数にならない。
k=2のとき、8n=200、n=25
a=2×25-1=49 b=49+2=51
a=49、b=51
k=4をいれると、8n=400、n=50となり、
a=99、b=101と題意に適さなくなる。
(8) 50.1%
説明記述付き。1個ずつ丁寧に処理をする。
A(t、3t+2)⇒AB=3t+2
DE=ABより、Dのx座標はt-(3t+2)=-2t-2
これとy軸に線対称の関係にあるCのx座標は2t+2
EC=(2t+2)-t=t+2
一方、Cはm上の点なので、y=1/8x2に代入して、
Cの座標は(2t+2、1/2t2+t+1/2)
CF=1/2t2+t+1/2
EC=CFより、t+2=1/2t2+t+1/2
t>0で、t=√3
大問2(平面図形)
(1) 73.2%
扇形OABは、半径4cm、中心角がa度。
これらを円周の長さの公式にあてはめればいい。
4×2×π×a/360=πa/45cm
(2) 42.6%
FO=FCの証明。
辺の情報が乏しいので、角度から攻める。

△ACDは二等辺三角形なので、
∠CAD=∠CDA=●とおく。
円周角定理と外角定理で2角が等しい⇒△FOCは二等辺⇒FO=FC
(3)① 33.6%

△AOC∽△OFCに気づけるかどうか。
△AOCも2つの半径から二等辺である。
OC:CA=FC:CO=4:6
FC=4×4/6=8/3cm
② 22.7%!
前問より、FC=8/3
AF=6-8/3=10/3

△ABCで三平方→AB=2√7
△ABC⇒△AOC⇒△AOFの順で面積をしぼっていく。
6×2√7÷2×1/2×10/18=5√7/3cm2
大問3(空間図形)
(1)① 74.3%
四角形ADEBは等脚台形。
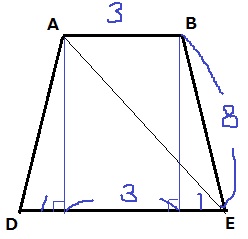
△AEBの高さは、√(82-12)=√63=3√7cm
3×3√7÷2=9√7/2cm2
② 74.5%
△ADEに着目。
DG:GE=2:3
HG//AEから、DH:HA=2:3(平行線と線分の比)
AH=8×3/5=24/5cm
③ 18.2%!
△ACDに着目。
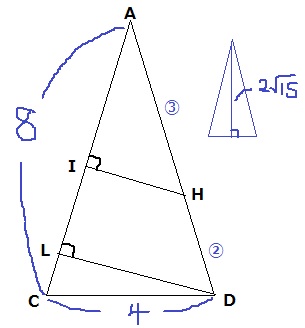
DからACに垂線をおろし、交点をLとおく。
LDがでれば、△ALD∽△AIHからIHがでる。
LDは△ACDにおいてACを底辺としたときの高さ。
底辺をCDとおいたときの△ACDの高さは三平方から2√15。
底辺CD→底辺ACは4→8と2倍になるので、高さは2√15→√15
LD=√15cm
IH=√15×3/5=3√15/5cm
(2)① 67.3%
四角形ADEBをピックアップ。
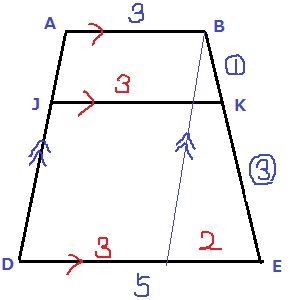
AB//JK//DE、BK:KE=2:6=1:3
Bを通るADに平行な補助線をひいて、
JK=3+2×1/4=7/2cm
ここまでは正解しておきたい。
② 12.7%!

まずは全体の高さを調べる。
DEに平行で同じ長さになるまでABを延長。
(図形全体を三角柱にする)
AM=(5-3)÷2=1cm
△AMDで三平方→MD=3√7cm
△MNDで三平方→MN=√59cm(全体の高さ)
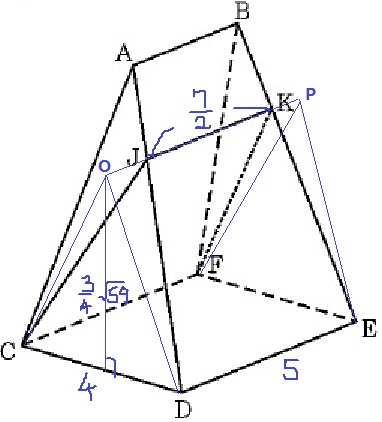
JKの延長線上で、垂線をおろすとCDに交わる点をOとする。
OとCDとの距離はAD:JD=4:3より、√59×3/4=3√59/4cm
断頭三角柱で体積を求める。
底面は△OCD…4×3√59/4÷2=3√59/2cm2
高さはJK・CF・DEの平均…(7/2+5+5)÷3=9/2cm
求積すべき立体の体積は、3√59/2×9/2=27√59/4cm3



コメント