2020年度　浅野中学過去問【算数】大問４解説

問題ＰＤＦ
長さ３ｃｍの１本の細いひもがあり、その両端を点Ｐ、点Ｑとします。
このとき、次の〔　ア　〕～〔　ウ　〕にあてはまる数をそれぞれ求めなさい。
ただし、球の体積は、（半径）×（半径）×（半径）×（円周率）×４÷３で求められます。
また、ひもは太さを考えず、伸び縮みしないものとします。

（１）
〔図９〕のように、点Ｐを平らな床の面に固定します。
このとき、点Ｑが動ける範囲の体積は、〔　ア　〕×3.14ｃｍ³となります。

（２）
〔図10〕のように、縦３ｃｍ、横３ｃｍ、高さ４ｃｍの直方体が平らな床の面に置かれています。
点Ｐを直方体の頂点Ａに固定します。
このとき、点Ｑが動ける範囲の体積は、〔　イ　〕×3.14ｃｍ³となります。

（３）
〔図11〕のように、縦３ｃｍ、横３ｃｍ、高さ４ｃｍの直方体が平らな床の面に置かれています。
点Ｐを辺ＡＢ上で動かします。
このとき、点Ｑが動ける範囲の体積は、〔　ウ　〕×3.14ｃｍ³となります。

＠解説＠
（１）

ドーム状（半球）になる。
半球は球の半分なので、３×３×３×3.14×４÷３÷２＝18×3.14
ア…18

（２）

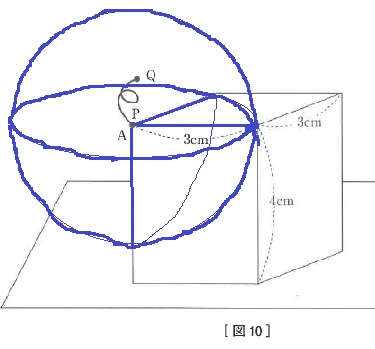
球の８分の１が直方体に食われる。
求積すべきは、球の８分の７にあたる。
３×３×３×3.14×４÷３×７/８＝31.5×3.14
イ…31.5

（３）

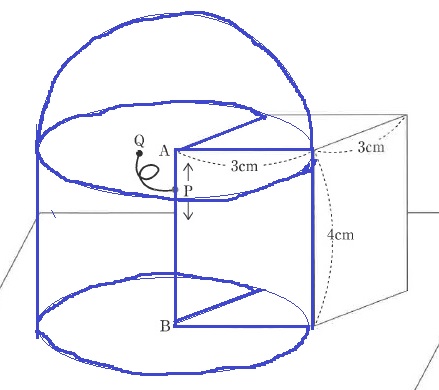
半球＋中心角270°の円柱。
18×3.14＋３×３×3.14×３/４×４
＝18×3.14＋27×3.14＝45×3.14
ウ…45
難関中（算数科）解説ページに戻る