2020年度　麗澤中学過去問【算数】大問２解説

問題ＰＤＦ
次の〔　　〕にあてはまる数を答えなさい。
（１）
濃度６％の食塩水250ｇと濃度10％の食塩水〔　　〕ｇと水50ｇを混ぜると、
濃度７％の食塩水になりました。

（２）
麗太くんと麗子さんは、南柏駅から〔　　〕ｋｍの一直線の道を通って麗澤中学校に向かうため、
麗太くんは分速100ｍで歩き、麗子さんは時速30ｋｍで進むバスに乗りました。
麗子さんの乗ったバスは、途中にある３つの信号で、それぞれ２分ずつ停車しました。
２人は同時に出発しましたが、麗太くんは麗子さんよりも10分遅れて麗澤中学校に到着しました。

（３）
あるファストフード店では、店内で食べる物には10％の消費税が、
持ち帰るものには８％の消費税がかかります。麗太くんは店内で定価290円のポテトを食べ、
定価〔　　〕円のハンバーガーを持ち帰ったので697円かかりました。

（４）
身長が全員ことなる５人を以下の規則にしたがって一列に並ばせるとき、
並び方は全部で〔　　〕通りあります。
規則：左から２番目と４番目の人はどちらも、両隣りの人より背が高い。

（５）
下の数字の列はある規則性にしたがって並んでいます。
〔　　〕に入る数を答えなさい。

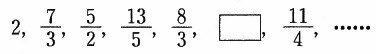
（６）
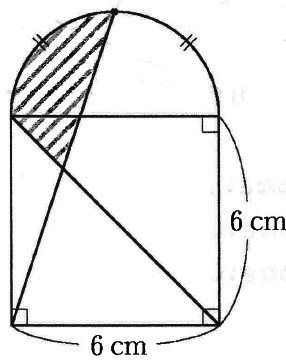
下の図の斜線部分の面積は〔　　〕ｃｍ²です。
ただし、円周率は3.14とします。

＠解説＠
（１）
先に、濃度６％食塩水250ｇと水50ｇを混ぜてしまおう。
食塩の量は250×６％＝15ｇ
食塩水の量は250＋50＝300ｇ
水50ｇを混ぜた後の濃度は、15÷300×100＝５％

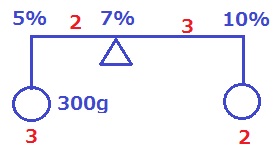
ここで天秤法を使う。
支点からの距離が２：３なので、おもりの重さは３：２。
300×２/３＝200ｇ

（２）
時速30ｋｍを分速に変換。
麗子の速さ…30×1000÷60＝分速500ｍ
速さの比は、麗太：麗子＝100：500＝１：５
時間の比は逆比で、麗太：麗子＝⑤：①

麗子のバスは途中で合計６分間停車し、麗太は麗子の10分遅れで到着。
→もし、信号がすべて青でバスの停車がなかったら、麗太は16分遅れになっていた。
時間の比の差④が16分だから、麗子の時間①は４分。
南柏駅～麗澤中学までは、分速500ｍ×４分＝2000ｍ＝２ｋｍ
*実際どうなのか地図で調べてみたら、２ｋｍほどの距離でした。

（３）
店内のポテトは税込みで、290×110％＝319円
残りは、697－319＝378円
持ち帰ったハンバーガーの定価は、378×100/108＝350円

（４）

最も背が高い人を２番に配置。
２番目に高い人を１番に配置すると、３番目に高い人は４番にくる。
２通り

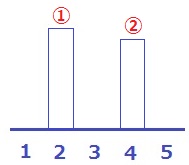
今度は、２番目に高い人を４番に配置する。
残り３人はどこでもいい。
３×２×１＝６通り
計８通り

最も背が高い人を４番に配置しても同様のことがいえる。
対称的に考えて、８×２＝16通り

（５）

整数を分数に変え、既約分数が約分されたと仮定すると…
分子が３、分母が１ずつ増えていた。
19/７

（６）

半円の中心点を意識しよう。青線の直角三角形が相似。
底辺：高さ＝１：３から、小さい直角三角形の底辺が１ｃｍ。その左が２ｃｍ。

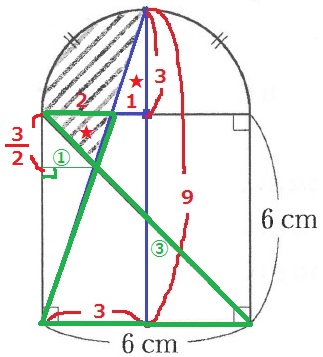
緑線の三角形で相似。
辺の比が２：６＝１：３
上の三角形の高さは、６×①/④＝３/２ｃｍ
★の面積を調べてみると…１×３÷２＝３/２ｃｍ²
２×３/２÷２＝３/２ｃｍ²で面積が等しい。
移植すると、半径３ｃｍの４分の１円になる。
３×３×3.14÷４＝7.065ｃｍ²

＠別解＠

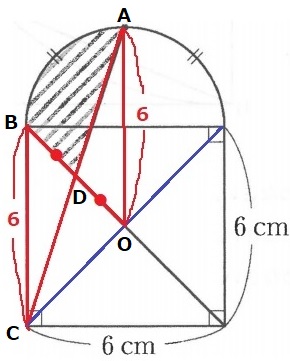
正方形の対角線Оは正方形の中心。
ＡＯ＝３＋３＝６ｃｍ
△ＡＯＤと△ＣＢＤは１辺と両端角が等しく合同。
ＢＤ＝ＤＯ

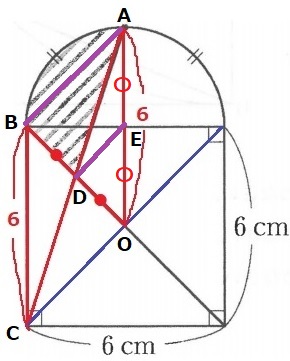
△ＯＢＥは直角二等辺三角形で、ＥＡ＝ＥＯ＝３ｃｍ
ＯＥ：ＥＡ＝１：１
△ＯＤＥと△ＯＢＡで、ＯＤ：ＤＢ＝ＯＥ：ＥＡ＝１：１
平行線と線分の比（中点連結定理）からＢＡ//ＤＥ（平行）

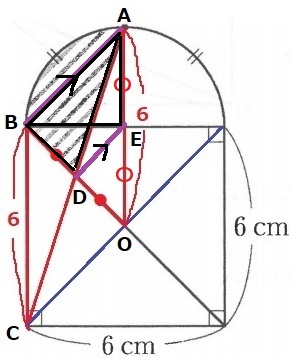
等積変形で△ＡＢＤと△ＡＢＥの面積が等しい。
→求積すべき図形は半径３ｃｍの４分の１円に変形できる。
３×３×3.14÷４＝7.065ｃｍ²
難関中（算数科）解説ページに戻る