2020年度　本郷中学過去問【算数】大問４解説

問題ＰＤＦ
Ｈ君とＲ君は本郷中学校の生徒です。
二人は協力して以下の問題を解こうとしています。

Ｈ君「なんだか難しそうだね」
Ｒ君「一緒に考えてみようよ」
Ｈ君「そうだね、まずはいろいろ試してみようか。
うーん、頂点Ｃは通らずに、頂点Ｄを２回経由して最後に頂点Ａに到達する経路は何本だろう？」
Ｒ君「それは･･･ｘ本だね！」

（１）ｘの値を答えなさい。

Ｈ君「なるほどね。じゃあ、頂点Ｃを通らずに、移動し始めてから３回頂点Ａを経由して
最後に頂点Ａに到達する経路は何本だろう？」
Ｒ君「今度はこうだから･･･ｙ本だね！」

（２）ｙの値を答えなさい。

Ｈ君「Ｒ君、もっとわかりやすく考えていくにはどうすればいいの？」
Ｒ君「こういうときには図をかくといいよ！」
Ｈ君「そうか、そしてここに頂点Ｃを通らないような経路を矢印で記入するんだね」
と言って二人は次の図をかきはじめました。

Ｒ君「そう、必要な矢印をかき終えたら、ここは１、ここも１、こことここの和で２、
のように小さく隅に数字を書きそえて…」
Ｈ君「最後にここの和を求めて、全部でｚ本だ！」
Ｒ君「そうだね！やったね！！」

（３）ｘの値を答えなさい。

＠解説＠
（１）

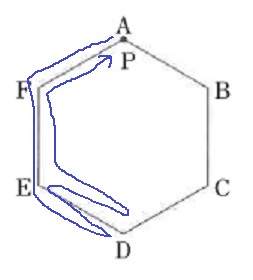
Ｄを２回経由してＡに戻るには、Ａ→Ｆ→Ｅ→Ｄ→Ｅ→Ｄ→Ｅ→Ｆ→Ａしかない。
ｘ＝１

（２）

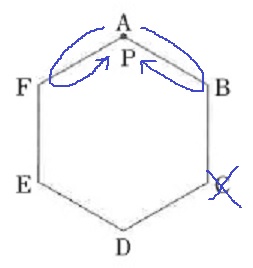
ゴールを含め、８回の移動でＡに４回触れるには、
Ａの隣にあるＢかＦに行ってＡに戻るしかない（Ｅには行かない）。
Ａ→ＢorＦ→Ａ→ＢorＦ→Ａ→ＢorＦ→Ａ→ＢorＦ→Ａ
２×２×２×２＝16通り
ｙ＝16

（３）

Ｃには行かないので、上はＤ、下はＢで終わり。
ジクザグの矢印を書き、おなじみの方法で数字を足していく。
ｚ＝41

＠＠
本郷の過去問ページより、受験者452名中の正解者数。
（１）274名（２）36名（３）106名
（２）の正答率が悪い！
ゴール時に頂点Ａには３回ではなく４回触れることになる。
難関中（算数科）解説ページに戻る