平均25.39点（50点満点、前年比；－1.32点）
問題はコチラ→ＰＤＦファイル
大問１（計算）
（１）ア 96.5％
５＋（－３）×８
＝５－24＝－19
イ 96.5％
（45ａ2－18ａｂ）÷９ａ ←分配法則
＝45ａ2÷９ａ－18ａｂ÷９ａ
＝５ａ－２ｂ
ウ 92.3％
（ｘ－ｙ）/２－（ｘ＋３ｙ）/７
＝｛７（ｘ－ｙ）－２（ｘ＋３ｙ）｝/14
＝（５ｘ－13）/14
エ 95.1％
42/√７＋√63
＝６√７＋３√７
＝９√７
（２） 82.0％
（３ａ＋４）2－９ａ（ａ＋２）
＝９ａ2＋24ａ＋16－９ａ2－18ａ
＝６ａ＋16 ←ここで代入
＝６×７/６＋16
＝23
（３） 90.3％
ｘ2＋ｘ＝21＋５ｘ
ｘ2－４ｘ－21
＝（ｘ－７）（ｘ＋３）＝０
ｘ＝－３、７
大問２（小問集合）
（１） 75.9％
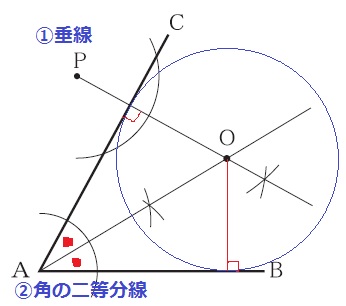
作図問題。
①Ｐを通る、辺ＡＣに垂直な線分。
②辺ＡＢ、ＡＣに接する→円の中心Ｏは∠ＣＡＢの二等分線上にある。
（２） 57.2％
扇形の半径は円錐の母線。
【側面の扇形の中心角＝360°×円錐の底辺の半径/母線】
360×２/５＝144°
（３） 38.1％
６枚から２枚を選ぶ→6Ｃ2＝15通り
公約数が１つしかない（互いに素）組み合わせを調べる。
１をとると２～６→５通り
２をとると３・５→２通り
３をとると４・５→２通り
４をとると５→１通り
５をとると６→１通り
計11通り。
したがって、確率は11/15
大問３（データの活用）
（１） 39.0％
最頻値（モード）→最もよくあらわれた値。
７
（２） 19.6％！
ａを除いたデータを昇順になおすと、〔４・６・７・７・７・７・10・10・13・15・16〕
11個の中央値（メジアン）は、（11＋１）÷２＝６番目→最後の７
12個の中央値（メジアン）は６番目と７番目の平均。
平均が8.5ということは、６番目と７番目の数字の和が8.5×２＝17
つまり、６番目が７、７番目が10になればいい。
ａが10未満だと中央値は8.5未満になってしまう→ａの最小値は10
範囲（レンジ；最大値と最小値の差）は12日なので、ａの最大値は４＋12＝16日
10≦ａ≦16
大問４（方程式）
連立方程式。 50.8％
大人をｘ、子供をｙ人とする。
人数と入館料で方程式をつくる。
ｘ＋ｙ＝183 …①
大人は65歳未満は0.8ｘ人、65歳以上は0.2ｘ人と分け、
65歳以上の入館料は500×９/10＝450円で計算。
500×0.8ｘ＋450×0.2ｘ＋300ｙ＝76750
490ｘ＋300ｙ＝76750 …②
②－①×300
490ｘ＋300ｙ＝76750
－)300ｘ＋300ｙ＝54900
190ｘ ＝21850
ｘ＝115
①より、ｙ＝183－115＝68
大人は115人、子供は68人。
大問５（空間図形）
（１） 79.6％
ネジレの位置→平行でもない、かつ交わらない。
ＢＣ・ＦＧ・ＣＤ・ＧＨ
このなかで、面ＡＢＣＤと平行なのは辺ＦＧと辺ＧＨ。
（２） 66.7％
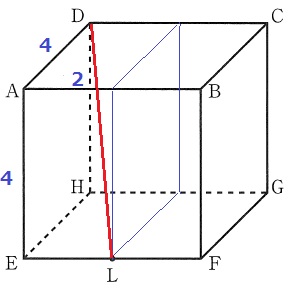
１辺の長さがａ、ｂ、ｃの直方体の対角線の長さ→√（ａ2＋ｂ2＋ｃ2）
√（２2＋４2＋４2）＝６ｃｍ
（３） 9.0％!!
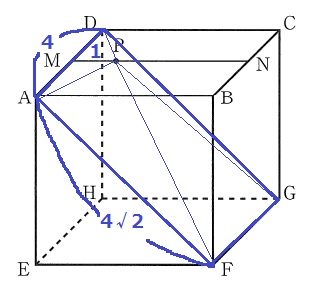
図示するとこうなる。
△ＡＢＦは直角二等辺三角形。１：１：√２からＡＦ＝４√２
底面は長方形ＡＦＧＤとして、問題は高さ。
四角錘Ｎ－ＡＦＧＤとの高さの比から考えてみる。
正面ＡＥＦＢから眺めると、Ｎ－ＡＦＧＤ：Ｐ－ＡＦＧＤの高さの比＝ＭＮ：ＭＰ＝④：①
④は正方形の対角線ＡＦの半分で２√２。
したがって、Ｐ－ＡＦＧＤの体積は、４×４√２×２√２×１/４×１/３＝16/３ｃｍ3
大問６（関数）
（１） 73.4％
反比例。
ｘとｙの積は比例定数ａで一定。
Ａ座標より、ａ＝２×（－６）＝－12
ｙ＝－12/ｘ
（２） 53.2％
変化の割合＝（ｙの増加量）/（ｘの増加量）
｛（－２）2ａ－（－５）2ａ｝/｛－２－（－５）｝
＝－21ａ/３＝－７ａ
*ｙ＝ａｘ2のグラフにおいて、ｘの値がｐからｑに変化するときの変化の割合はａ（ｐ＋ｑ）
ａ×（－５－２）＝－７ａ
（３） 11.2％！
説明の記述まで要求されるので大変:;(∩´＿`∩);:
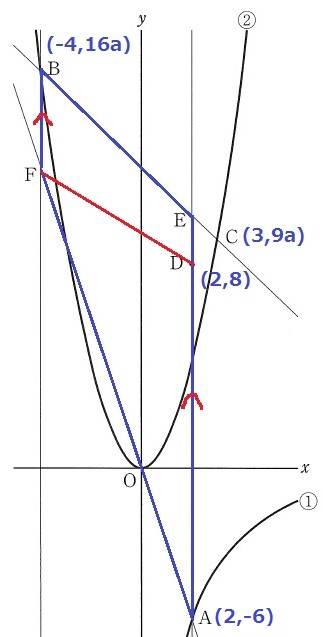
ｙ＝ａｘ2に代入してＢ（－４、16ａ）Ｃ（３、９ａ）
ＢＦとＥＡはｙ軸に平行。
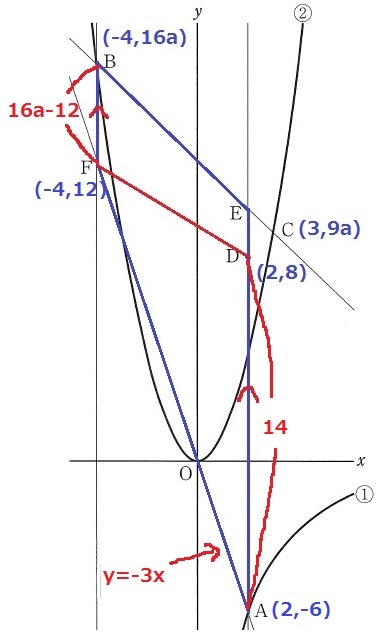
直線ＯＡの式は、ｙ＝－３ｘ
ｘ＝－４を代入して、Ｆ（－４、12）
ＡＤ＝８－（－６）＝14
ＤＦが台形ＢＦＡＥの面積を二等分するので、
ＡＤ＝ＢＦ＋ＤＥ（上底と下底の和）
すなわち、ＢＦ＋ＤＥ＝14となればいい。
ＢＦ＝16ａ－12
Ｅ座標を知るために、直線ＢＣに目をつける。
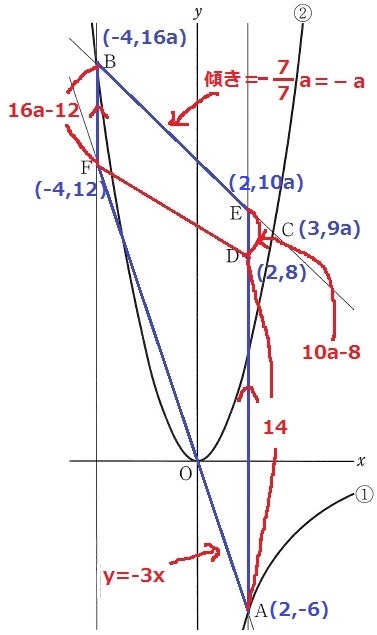
Ｂ（－４、16ａ）→Ｃ（３、９ａ）
右に７、下に－７ａなので、傾きは－７/７ａ＝－ａ
Ｃから左に１いくと、上に＋ａでＥ。
ここからＥ（３、10ａ）
ＥＤ＝10ａ－８
ＢＦ＋ＤＥ＝（16ａ－12）＋（10ａ－８）
＝26ａ－20＝14
26ａ＝34
ａ＝17/13
大問７（平面図形）
（１） 22.2％！
△ＢＣＦ∽△ＡＤＥの証明。
けっこう段階があります(;´Д｀)
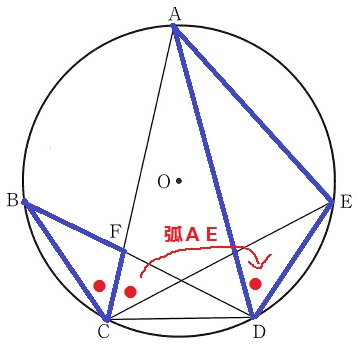
仮定と弧ＡＥに対する円周角から、∠ＢＣＦ＝∠ＡＤＥ
問題はもう１つの角。。
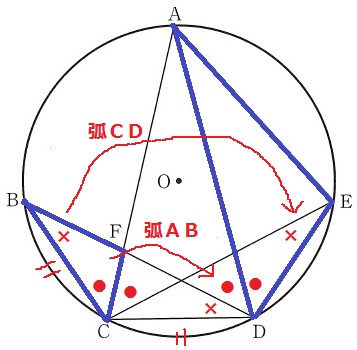
弧ＡＢに対する円周角より、∠ＡＤＢ＝●
弧の長さが等しければ円周角も等しい。
弧ＢＣ＝弧ＣＤより、∠ＣＢＤ＝∠ＢＤＣ＝∠ＣＥＤ＝×
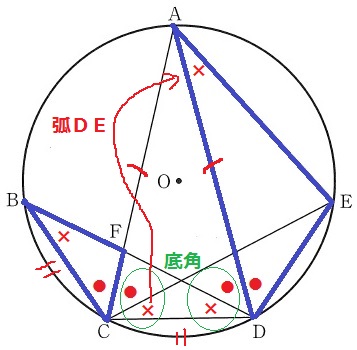
ここで△ＡＣＤが二等辺であることを利用する。
底角が等しいので∠ＡＣＤ＝∠ＡＤＣ
∠ＡＣＤ＝●＋∠ＥＣＤ
∠ＡＤＣ＝●＋×
ここから、∠ＥＣＤ＝×となる。
弧ＤＥに対する円周角で、∠ＤＡＥ＝×
２角が等しいことから∽。
（２） 7.9％!!
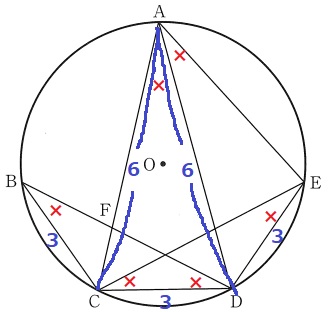
△ＡＣＤの二等辺より、ＡＣ＝６ｃｍ
（１）の等角をみると、弧ＤＥに対する円周角である∠ＤＡＥ＝×に注目。
円周角が等しい→（同じ円であれば）弧が等しく、弦も等しい。
ＤＥ＝３
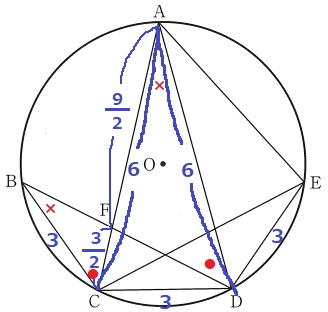
（１）の△ＢＣＦ∽△ＡＤＥを用いる。
ＢＣ：ＣＦ＝ＡＤ：ＤＥ＝６：３＝２：１
ＣＦ＝３÷２＝３/２
ＡＦ＝６－３/２＝９/２
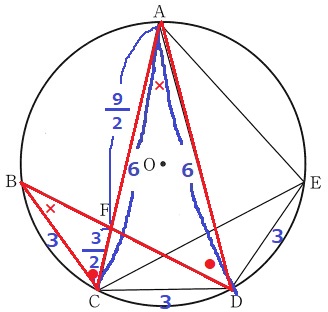
２角相等より、△ＢＣＦ∽△ＡＤＦ
ＢＦ＝９/２×３/６＝９/４ｃｍ
以下、公式の検査結果を参照。
大問１
基礎的な計算問題は正答率が良い◎ケアレスが怖い。
大問２
（２）半径/母線の公式で１発だが、なぜそうなるかも押さえておきたい。
誤答では150が多かった。
（３）場合分けで整理して調べる。誤答は１/３や２/５。
大問３
（１）モードはやりやすいと思うのだが。。
（２）中央値を丁寧に扱うこと！範囲の認定も雑にやらない。
誤答は４≦ａ≦16や７≦ａ≦10が見られた。
大問４
方程式の記述問題。過半数が正答〇
『数量関係の正しい立式ができていないものが多い。
また、どのような数量をｘやｙで表しているのか明記していないのも目立つ』
大問５
（２）誤答は２√５が見られた。
（３）錘の高さを正面から見た平面で捉える。無答も多かった。
大問６
（２）誤答では変化の割合ではなく、変域を解答したものが目立つ。
（３）説明しにくい設問だと思うが、正答率は11.2％であった。
『点座標を正しく求められないための誤答が多く、無答も多かった』
おそらく、傾きとｙ座標にａが入るＥの処理が難しかったと思われる。
大問７
（１）相似の証明。ここも説明しづらいが、２割超も正答者がいた。
解説では●、×で書いたが、実際の答案作成では記号で書かなくてはならない。
（２）前問の相似に目をつけたい。かといって、ＡＥにこだわりすぎるのは×。
ちなみに、コロナ禍における出題範囲の縮小はなしとのこと。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント
ありがとうございます。今年静大附属に中受で合格した子の母です。高校は浜松なのか、都内かまだ私の勤務地によるのでわかりません。
都内ならば、都立も対策しなくてはならないのでこのブログは貴重でありがたいです。
数学、特に証明は得意分野だったのですが、このレベルも解けなくなったのかーと自分でショックでした。手数を考える根気がなくなってたか。当たり前ですが他は解けました。中学受験の為にリハビリしたあとですから。
自分も彼女の大学受験に備えてリハビリしつつ、子の事は先ずはプロにマネジメントして貰おうと思います。
コメントありがとうございます。
静大附属中合格おめでとうございます(*’ω’*)
中受を乗り越えられた娘さんであれば、高受に求められる学力は問題なく吸収できると思います。
都立の数学は大問２と大問４（１）、理社にも特徴が見受けられますが、
基礎学力の定着さえあれば、過去問は少しの体験で打破できます。
いつでもいらして下さい(´ω｀)