2020年度　高知県公立高校入試過去問Ａ日程【数学】解説

平均19.0点（前年比；＋0.5点）

満点０人、０点49人。
問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）①　94.4％
－５－４＋７
＝－２

②　62.2％
（２ｘ＋ｙ）/４－（ｘ－２ｙ）/６
＝｛３（２ｘ＋ｙ）－２（ｘ－２ｙ）｝/12
＝（６ｘ＋３ｙ－２ｘ＋４ｙ）/12
＝（４ｘ＋７ｙ）/12

③　56.8％
24ａ²ｂ²÷（－６ｂ³）÷２ａｂ
＝－２ａ/ｂ²

④　86.8％
√75－９/√３
＝５√３－３√３
＝２√３

（２）　38.3％
２（５＋ｂ）＝ａ
10＋２ｂ＝ａ
２ｂ＝ａ－10
ｂ＝（ａ－10）/２

（３）　8.3％!!（無解答25.6％）
４％の食塩水をｘｇとする。９％の食塩水は600－ｘｇ
食塩で等式を作成。
４/100ｘ＋９/100（600－ｘ）＝600×６/100　←100倍
４ｘ＋９（600－ｘ）＝600×６
５ｘ＝1800
ｘ＝360　→360ｇ

＠別解＠
中学受験の必殺ワザ、天秤法。

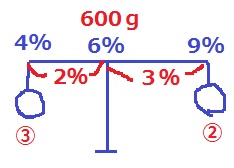
４％と９％を混ぜたら６％になった。
６％を支点として天秤をつくる。
支点からの距離は２：３だから、重りの重さは３：２。
600ｇを３：２に案文して、600×３/５＝360ｇ

（４）　56.1％
因数分解が出来ないので解の公式。
ｘ＝（－７±√41）/４

（５）　46.6％
ｙ＝－ｘ²は上に凸のグラフ。
ｘの変域から原点を通過するので、ｘ＝０のとき最大値ｙ＝０
最小値は原点から最も離れたｘ＝３のとき、ｙ＝－９
－９≦ｙ≦０
ａ…－９、ｂ…０

（６）　36.1％
半径は６ｃｍ。
球の体積…Ｖ＝４/３πｒ³
４/３π×６³＝288πｃｍ³

（７）　45.1％
ありがたいことに平均値ａが提供されている。
40人の中央値（メジアン）ｂは20番目と21番目の平均値→共に２～３の階級で階級値2.5。
最頻値（モード）ｃは最も現れている値→１～２の階級で階級値は1.5。
ｃ（1.5）＜ｂ（2.5）＜ａ（3.3）

（８）　12.4％！（部分点0.2％）
作図問題。
①∠ＡＢＣの二等分線。
②Ａを通る、①の二等分線に垂直な線分。
交点がＰとなる。

大問２（整数）

（１）　76.6％
連続する４つの奇数において、最小の奇数を２ｎ＋１とする。
これに＋２、＋４、＋６をすれば、連続する奇数になる。
ア…２ｎ＋３、イ…２ｎ＋５、ウ…２ｎ＋７

（２）　38.3％
連続する５つの整数において、３番目に大きい整数をｎとすると、
５つの整数はｎ－２、ｎ－１、ｎ、ｎ＋１、ｎ＋２となる。
（ｎー２）＋（ｎ－１）＋ｎ＋（ｎ＋１）＋（ｎ＋２）
＝５ｎ＝280
ｎ＝56
最も小さい整数は、ｎ－２＝56－２＝54

（３）　24.9％！（部分点16.3％、無答35.1％）
連続する３つの偶数の和で『表すことができない』証明。
通常通り、文字式を立てて変形し、最後のｎが割り切れない→表すことができない、という流れ。

連続する３つの偶数において、真ん中の偶数を２ｎ（ｎは整数）とおくと、
連続する３つの偶数は２ｎ－２、２ｎ、２ｎ＋２となる。
（２ｎ－２）＋２ｎ＋（２ｎ＋２）
＝６ｎ＝280
ｎ＝140/３
ｎが整数ではないので、２ｎ－２、２ｎ、２ｎ＋２は偶数ではない。
したがって、280は連続する３つの偶数の和で表すことができない。
（偶数・奇数は整数の話。ｎが整数でなければ、２ｎ－２などは整数でない＝偶数でない。
仮定と矛盾するので、”表せない”ことが証明できる。最後は問いに答える形でフィニッシュ）

大問３（平面図形１）

（１）　15.1％！（部分点7.6％、無答41.9％）
∠ｘ＋∠ｙ＝90°の証明。

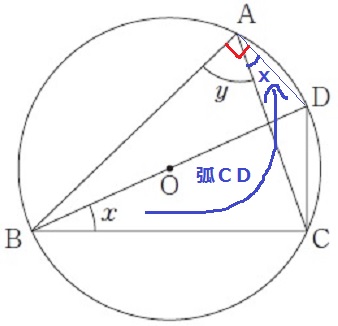
ＡＤに補助線。
弧ＣＤに対する円周角より、∠ＣＡＤ＝∠ｘ
直径に対する円周角は90°であるのを利用し、∠ＢＡＤ＝∠ｘ＋∠ｙ＝90°

（２）　12.4％！

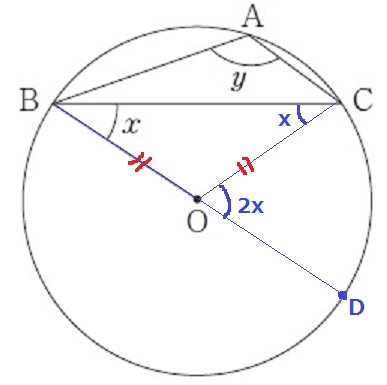
ＯＣに補助線。
半径からＯＢ＝ＯＣより、△ＯＢＣは二等辺。
∠ＯＣＢ＝∠ｘ

ＢＯを延長して、円周との交点をＤとする。
△ＯＢＣの外角定理で、∠ＣＯＤ＝∠ｘ＋∠ｘ＝２∠ｘ
（∠ＣＯＤが∠ＣＢＤの中心角である点を指摘しても良い）

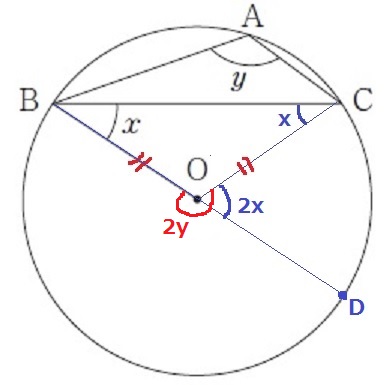
∠ｙは、Ａを含まない弧ＢＣに対する円周角。
その中心角である∠ＢＯＣ＝２∠ｙ

ＢＤが直線であることから、
２∠ｙ－２∠ｘ＝180°　←すべての項を÷２
∠ｙ－∠ｘ＝90°

＠別解＠

公式より。ＡＤに補助線。円周角で∠ｘを∠ＤＡＣに移す。
直径に対する円周角で∠ＢＡＤ＝90°から、∠ｙ＝∠ｘ＋90°
こちらの方が筋道がスッキリしていますね。

＠余談＠

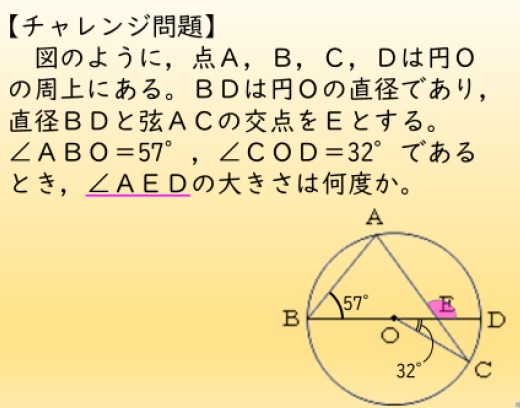
チャレンジ問題がくっついていたのでやってみました。

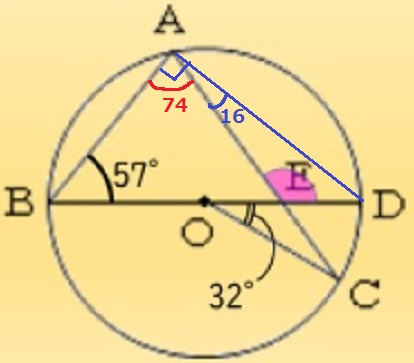
円周角で∠ＣＡＤ＝32÷２＝16°
直径に対する円周角から引く。∠ＢＡＥ＝90－16＝74°
△ＡＢＥで外角定理→∠ＡＥＤ＝74＋57＝131°

大問４（確率）

（１）　43.9％
１回目に１枚、２回目に５枚裏返せば、６枚すべて黒。
つまり、１回目の数＋２回目の数＝６になればいい。
（１、５）（２、４）（３、３）（４、２）（５、１）
以上、５通り→５/36

（２）　21.5％！
こまＥが白となるパターンを考える。
■１回目と２回目でＥを裏返すパターン
→１回目に５か６を出す⇒２通り
２回目は２以上でＥが裏返る⇒５通り
２×５＝10通り

■Ｅを１度も裏返さないパターン
→２回目は１しか出さない⇒１通り
１回目は１～４の範囲まで⇒４通り
１×４＝４通り

計14通り
14/36＝７/18

大問５（関数）

（１）　77.3％
ｙ＝１/４ｘ²に、ｘ＝－６を代入。
ｙ＝１/４×（－６）²＝９
Ａ（－６、９）

（２）　28.0％！
同様にＢの座標を求める→Ｂ（２、１）
ＡＣ＋ＣＢが最小ということは、ＡＣＢは一直線上にある。
言い換えれば、Ｃは直線ＡＢの切片にあたる。
Ａ（－６、９）→Ｂ（２、１）
右に８、下に８だから、傾きは－８/８＝－１
傾きが－１なので、Ｂから右に６、下に６移動して、Ｃ（０、３）

（３）　2.2％!!
回転体が２つある。

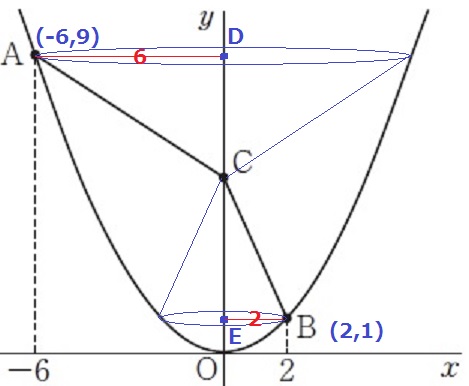
↑円錐がこのようにできる。

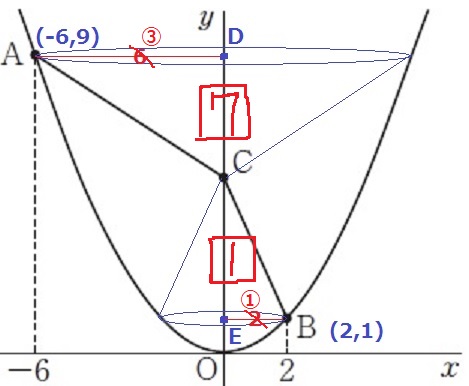
ＡＤ：ＢＥ＝６：２＝③：①
三角錐の体積比は底面積の比×高さで求められる。
③×③×ＤＣ＝①×①×ＣＥ×７
⑨×ＤＣ＝⑦×ＣＥ
ＤＣ：ＣＥ＝７：９

ＤＥ＝８なので、
ＣＥ＝８×９/16＝９/２

大問６（平面図形２）

（１）　4.4％!!（部分点27.1％、無答26.8％）
△ＡＤＥ≡△ＦＣＢの証明。
等辺がたくさんある。
△ＡＤＥと△ＦＣＢのどこの情報が知りたいか見極めること！

仮定より、ＡＤ＝ＦＣ
菱形の１辺より、ＤＥ＝ＣＢ
菱形ＢＣＥＤからＢＣ//ＤＥ、同位角で∠ＡＤＥ＝∠ＡＢＣ
△ＡＢＣは二等辺だから、∠ＡＢＣ＝∠ＦＣＢ
よって、∠ＡＤＥ＝∠ＤＣＢ
２辺とあいだの角が等しいので合同。

（２）　0.7％!!!
厄介(;´Д｀)
解法は複数あるが、ルート次第で処理の煩雑さが変わる。

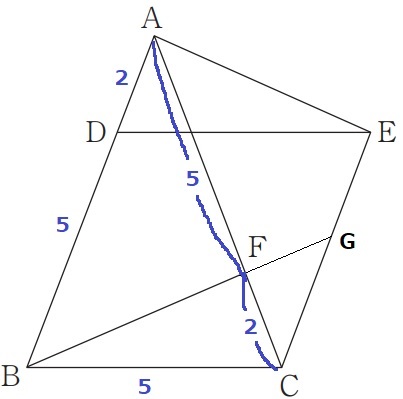
菱形の１辺は５ｃｍ。
ＡＢ＝７ｃｍより、ＡＤ＝７－５＝２ｃｍ
仮定より、ＦＣ＝２ｃｍ、ＡＦ＝７－２＝５ｃｍ

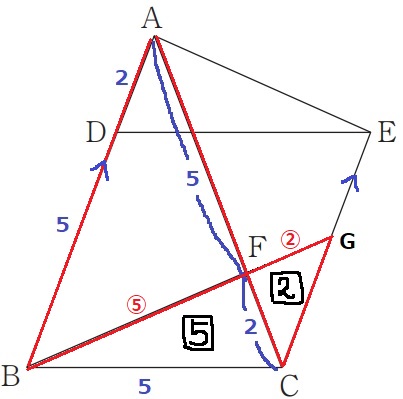
△ＡＢＦ∽△ＣＧＦより、ＢＦ：ＦＧ＝ＡＦ：ＦＣ＝⑤：②
△ＣＦＧの面積を【２】とすると、△ＣＦＢの面積は【５】となる。

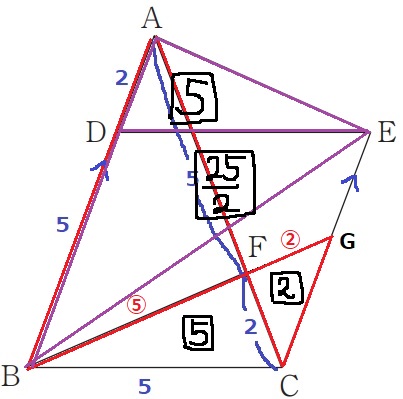
ここで前問の合同を使い、△ＥＡＤの面積も【５】。
ＡＤ：ＤＢ＝２：５より、△ＥＤＢ＝【５】×５/２＝【25/２】
△ＥＤＢは菱形ＢＣＥＤの半分なので、菱形ＢＣＥＤの面積は【25】
したがって、【25】÷【２】＝25/２倍