2021年度　広島県公立高校入試問題過去問【数学】解説

平均21.1点（前年比；－7.1点）

問題はコチラ→ＰＤＦファイル
出題範囲の縮小はなし。

大問１（小問集合）

（１）　83.9％
６－５－（－２）
＝６－５＋２
＝３

（２）　88.1％
６ａ²÷３ａ
＝２ａ　←代入
＝２×４
＝８

（３）　79.4％
√２×√６＋９/√３
＝２√３＋３√３
＝５√３

（４）　63.0％（部分正答1.3％）
ｘ²＋５ｘ－６
＝（ｘ＋６）（ｘ－１）
ｘ＝－６、１

（５）　72.5％
回転体は底面が半径３ｃｍの円、高さ５ｃｍの円錐。
３×３×π×５÷３＝15πｃｍ³

（６）　51.7％（部分正答0.2％）

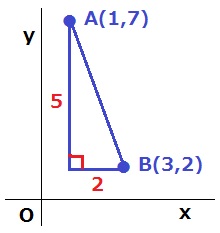
直角三角形を描く。
ＡＢ＝√（５²＋２²）＝√29

（７）　81.5％

2021年度秋田県大問２（１）②より。
ａ＞０は下に、ａ＜０は上に凸のグラフ。
ａの絶対値が大きくなるほどグラフの開きは小さくなる。
①…イ、②…ア、③…ウ

（８）　74.0％
全体…４×３＝12通り
和が６以上となる組み合わせは、（３、３）（４、２）（４、３）の３通り。
確率は３/12＝１/４

大問２（小問集合２）

（１）　35.9％（部分正答2.8％）
４＜√ａ＜13/３
ルートが邪魔なので、すべて２乗する。
16＜ａ＜169/９＝18・７/９
整数ａ＝17、18

（２）　23.1％！（部分正答24.8％、無答27.5％）
丁寧な処理が求められる。

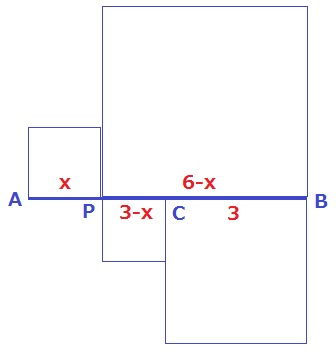
ＡＣ＝３ｃｍ→ＰＣ＝３－ｘｃｍ
上２つの正方形の面積は、
ｘ²＋（６－ｘ）²
＝ｘ²＋36－12ｘ＋ｘ²
＝２ｘ²－12ｘ＋36　…①

下２つの正方形の面積の２倍は、
２｛（３－ｘ）²＋３²｝
＝２（９－６ｘ＋ｘ²＋９）
＝２ｘ²－12ｘ＋36　…②
①＝②より、題意は示された。

（３）　12.8％！（無答27.4％）

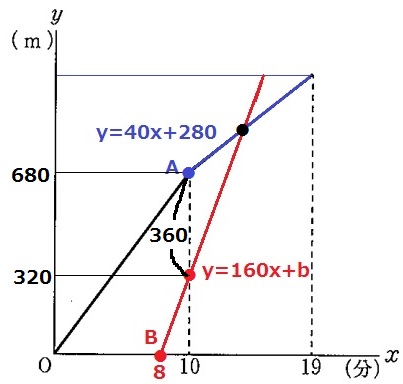
Ａが出発してから10分後の両者の位置を求める。
Ａ；40×10＋280＝680ｍ
Ｂ；160×２＝320ｍ
→ＢがＡに追いつくのは、Ａが坂道を歩いているとき。

10分後の両者の差は、680－320＝360ｍ
１分あたり、160－40＝120ｍずつ差が縮まるので、
360÷120＝３分後
Ｂが出発してから５分後だから、駅から160×５＝800ｍ

大問３（平面図形）

2.7％!!（無答17.5％）

ＢＤ//ＥＦ→△ＢＤＧ∽△ＦＥＧ
面積比は相似比の２乗だから、△ＢＤＧ：△ＦＥＧ＝㉕：④
△ＢＥＧ：△ＥＦＧ＝ＢＧ：ＧＦ＝５：２
△ＢＥＧ＝④×５/２＝⑩
ＡＤ//ＢＣの等積変形で、△ＡＢＥ＝△ＤＢＥ＝㉟
よって、△ＡＢＥ：△ＧＥＦ＝35：４

大問４（関数）

（１）　64.6％（部分正答0.4％）
ｙ＝８/ｘにｙ＝２を代入。
２＝８/ｘ
ｘ＝４
（*反比例の比例定数ａは積ｘｙで一定。ｘｙ＝８だから、ｘ＝８÷２＝４）

（２）　4.1％!!（無答40.4％）

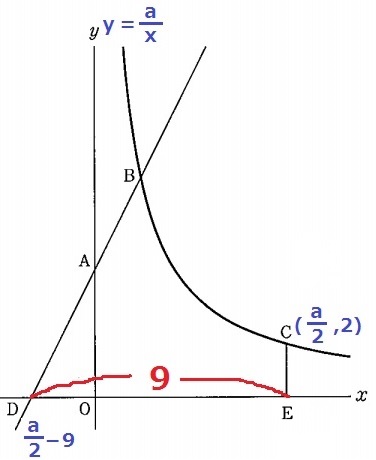
Ｃ座標から出発する。
ｙ＝ａ/ｘにｙ＝２を代入。
２＝ａ/ｘ
ｘ＝ａ/２
ＤＥ＝９より、Ｄのｘ座標はａ/２－９。

Ｂからｘ軸に垂線、足をＦとする。
△ＡＯＤ∽△ＢＦＤで、ＤＡ：ＡＢ＝ＤＯ：ＯＦ＝１：１
ＯはＤＦの中点⇒ＤとＦはｙ軸について対称関係にあるから、
Ｆ（Ｂ）のｘ座標は、－（ａ/２－９）＝－ａ/２＋９

一方で、Ｂのｙ座標はＡのｙ座標の２倍→ｙ＝10
これをｙ＝ａ/ｘに放り込むと、Ｂのｘ座標はａ/10。

Ｂのｘ座標で等式。
－ａ/２＋９＝ａ/10
－５ａ＋90＝ａ
ａ＝15

大問５（データの活用）

（１）　84.4％
範囲（レンジ；range）＝最大値－最小値
22.6万回－10.2万回＝12.4万回
ウ

（２）　28.0％！（部分正答13.0％）

他方より優秀な点を具体的な数値を示して述べればいい。
◆最頻値（モード）を比較すると、Ｙは23万回、Ｚは19万回。
Ｙに依頼した方がＡ市の動画の再生回数が増えそう。

Ｚを選ぶ場合、Ｙの10～20万あたりがＺより多いところに注目して、
再生回数の高いグループの合計がＺの方が多い点を指摘する。
◆再生回数が18万回以上の度数の合計を比較するとＹは26本、Ｚは33本。
Ｚに依頼した方がＡ市の動画の再生回数が増えそう。
（*再生回数が24万回以上のグループでも良い。
Ｚの最大値はＹより大きいが、50本のうちの３本だけなので極端な値を取り上げている。
根拠とする数値は外れ値を選択しない方が説得力はある）

大問６（平面図形）

（１）　13.5％！（部分正答16.6％、無答31.7％）
角の二等分線の作図方法の証明が狙われた。
ポイントは三角形の合同。

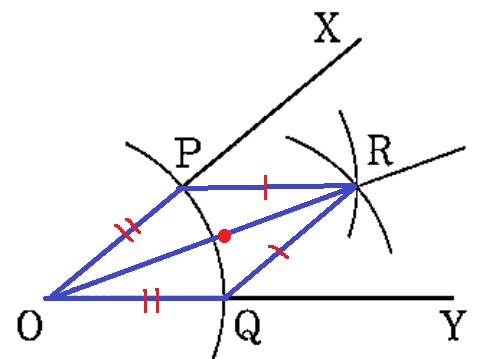
△ＰＯＲと△ＱＯＲにおいて、
ＯＰ＝ＯＱ、ＰＲ＝ＱＲ、共通辺ＯＲ
３辺が等しく△ＰＯＲ≡△ＱＯＲ
対応する角は等しいから、∠ＰＯＲ＝∠ＱＯＲ
よって、半直線ＯＲは∠ＸＯＹの二等分線である。
（*最後は証明したい内容でフィニッシュ！）

（２）　42.0％（部分正答0.4％）
垂線の作図。
普通はＩに針を合わせるが、別の方法で作図する。

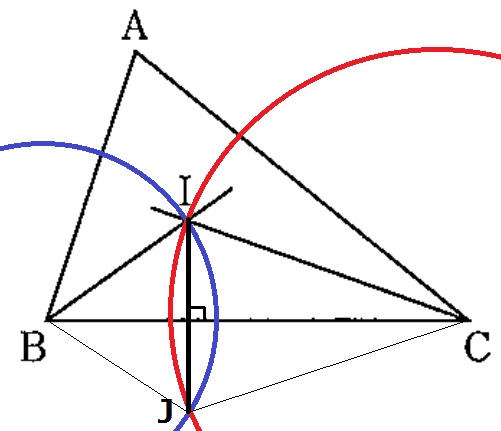
結論からいうと、
①Ｂを中心に半径ＢＩとする円を描く。
②Ｃを中心に半径ＣＩとする円を描く。
③ＩＪを引く。
すると、ＩＪ⊥ＢＣとなる。

なぜ、そうなるのか。ここも三角形の合同を用いる。
ＢＩ＝ＢＪ、ＣＩ＝ＣＪ、共通辺ＢＣより、３辺が等しく△ＢＣＩ≡△ＢＣＪ
ＢＣを対称の軸とするとＩとＪは対応する点であり、
対応する点同士を結んだ線分は対称の軸ＢＣと垂直に交わる。
ア…Ｂ、イ…ＢＩ、ウ…Ｃ、エ…ＣＩ

（３）　1.0％!!!（部分正答2.2％）
内接円を外接円とする三角形は必ず鋭角三角形である証明。

半径と接線は垂直に交わる。
∠ＩＦＡ＝∠ＩＥＡ＝90°
四角形ＡＦＩＥに注目すると∠ＩＦＡ＋∠ＩＥＡ＝180°
対角の和が180°だから、四角形ＡＦＩＥは円に内接する。
⇒∠ＦＡＥ＋∠ＦＩＥ＝180°なので、∠ＦＩＥ＝180－∠ｘ°

∠ＦＤＥは弧ＦＥに対する円周角だから、
∠ＦＤＥ＝（180－ｘ）÷２＝90－１/２∠ｘ°

∠ＦＤＥ＞０（０以下だと角を成さない）なので、90－１/２∠ｘは０より大きい。
また、90－１/２∠ｘ°は、90から１/２ｘを引いた値なので90°より小さい。
０＜90－１/２∠ｘ＜90
これが∠ＤＥＦ、∠ＥＦＤにもいえるので、△ＤＥＦは常に鋭角三角形となる。
オ…90－１/２∠ｘ、カ…０、キ…90

＠余談＠

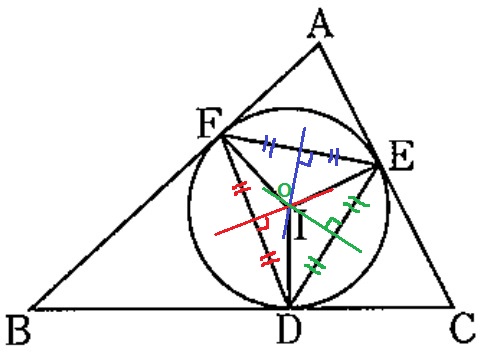
外接円の中心（外心）Ｏは、３辺の垂直二等分線の交点に位置する。
△ＤＥＦが鋭角三角形であれば、外心Ｏは△ＤＥＦの内部にある。

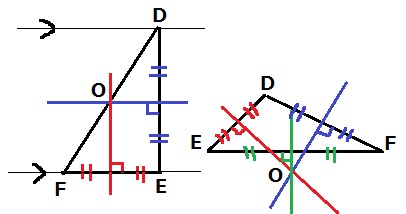
直角三角形の場合、外心Ｏは斜辺ＤＦの中点にくる。
ＥはＡＣ上、ＦはＡＢ上の点なので、ＡＢとＡＣが一直線になってしまい、△ＡＢＣを作れない。
鈍角三角形の外心Ｏは△ＤＥＦの外側にあらわれる。

大問５
設定が今風で面白い。こういう仕事もあるんだね(‘ω’)
（２）モードでいいと思う。
大問６
（１）中１で習う作図のはずなのに、その原理を完全に理解していた人は13.5％…。
コンパスの機能は等しい長さを移すことにあるので、等辺の活用でだいたいなんとかなる。
（２）なんとなく空欄の中身が想像できてしまう。理由の説明もできるように。
（３）鋭角＝直角より小さい角
∠ＦＤＥは０°より大きく、90°より小さくなければならない。
円に囲まれた図形は円周角。内接四角形がみえればＧＲＥＡＴ！

↑広島県教育委員会からのお達し。