2021年度　秋田県公立高校入試問題過去問【数学】解説

平均50.7点（前年比；－0.8点）

問題はコチラ→ＰＤＦファイル
出題範囲の縮小はなし。

大問１（小問集合）

指示された８問について答える。
（１）　82.2％
４－（－６）×２
＝４＋12
＝16

（２）　69.8％
（ｘ－２ｙ）/２－（３ｘ－ｙ）/６
＝｛３（ｘ－２ｙ）－（３ｘ－ｙ）｝/６
＝－５/６ｙ

（３）　56.1％
（ｘ－３ｙ）（ｘ＋４ｙ）－ｘｙ
＝ｘ²＋ｘｙ－12ｙ²－ｘｙ
＝ｘ²－12ｙ²

（４）　63.3％
ａ²＋２ａ
＝ａ（ａ＋２）　←代入
＝（√３－１）（√３＋１）
＝（√３）²－１²
＝３－１
＝２

（５）　70.8％
３/２ｘ＋１＝10
３/２ｘ＝９
ｘ＝９×２/３＝６

（６）　70.0％
紅茶450ｍLに混ぜるべき牛乳の量は、450×３/５＝270ｍL
足りない分は、270－180＝90ｍL

（７）　84.5％
ｘ＋４ｙ＝－１　…①
－２ｘ＋ｙ＝11　…②
①×２＋②をすると、９ｙ＝９
ｙ＝１
①に代入。ｘ＝－５
ｘ＝－５、ｙ＝１

（８）　79.0％
２ｘ²－５ｘ＋１＝０
解の公式を適用して、ｘ＝（５±√17）/４

（９）　83.3％
平均値…（１×１＋２×２＋３×３＋４×４＋５×６＋６×３＋７×１）÷20＝85÷20＝4.25冊
中央値…20人の場合、10番目と11番目の平均で4.5冊。
最頻値…５冊
ウ

（10）　34.2％
10＜√ｎ＜11　←２乗
100＜ｎ＜121
√（７ｎ）の根号を外すには、７ｎが平方数となればいい。
ｎ＝７では範囲外→ｎ＝７×（平方数）
100に近い７の倍数は105（＝７×15）
次の７の倍数は112（＝７×16）で16は平方数。
ｎ＝112

（11）　87.8％
外角定理より、ｘ＝44＋62＝106°

（12）　61.％
５×５×π×240/360＝50/３πｃｍ²

（13）　29.5％！

△ＡＢＯは正三角形→∠ＡＯＢ＝60°
この円周角にあたる∠ＡＣＢ＝60÷２＝30°
△ＡＢＣの内角より、∠ＢＡＣ＝180－（78＋30）＝72°

（14）　73.9％

（ＡＢを軸とした回転体）：（ＢＣを軸とした回転体）
＝（３×３×π×２×１/３）：（２×２×π×３×１/３）
＝６π：４π
＝３：２
３/２倍

（15）　10.7％！
立方体の体積が1000ｃｍ³⇒立方体の１辺は10ｃｍ。

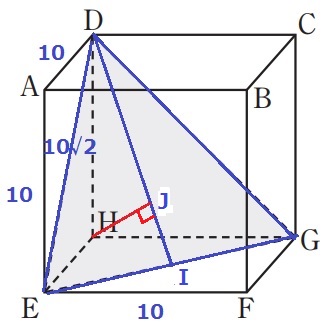
ＤからＥＧに垂線、足をＩとする。
ＨからＤＩに垂線、足をＪとする。
三角錐Ｈ―ＤＥＧの体積は、10×10÷２×10÷３＝500/３ｃｍ³

△ＡＤＥは１：１：√２の直角二等辺→ＤＥ＝10√２ｃｍ
△ＤＥＧの各辺は側面の正方形の対角線→いずれも10√２ｃｍの正三角形。
△ＤＥＩは１：２：√３の直角三角形→ＤＩ＝５√６ｃｍ
△ＤＥＧの面積は、10√２×５√６÷２＝50√３ｃｍ³
ＨＪ＝500/３×３÷50√３＝10√３/３ｃｍ

＠別解＠

立方体の対角線ＨＢ＝√（10²＋10²＋10²）＝10√３ｃｍ
断面ＤＨＦＢで捉える。
△ＤＢＪ∽△ＩＨＪで、ＤＪ：ＪＩ＝ＤＢ：ＩＨ＝２：１

正三角形ＤＥＧにおいて、ＩはＥＧの中点だからＤＩは中線。
中線ＤＩをＪは２：１に内分するので、Ｊは正三角形ＤＥＧの重心である。
そして、正三角錐Ｈ―ＤＥＧの頂点Ｈから底面の△ＤＥＧにひいた垂線の足は、
△ＤＥＧの重心Ｊと一致する。
ＨＪ：ＪＢ＝１：２だから、ＨＪ＝10√３×１/３＝10√３/３ｃｍ

大問２（小問集合２）

（１）①　58.2％
答案では求める過程も記述する。
ｘ＝１のとき、ｙ＝６
ｘ＝３のとき、ｙ＝２
変化の割合…（ｙの増加量）÷（ｘの増加量）
＝（２－６）÷（３－１）＝－２

②　28.0％！

ａ＞０で下に凸、ａ＜０で上に凸。
ａの絶対値が大きくなるほど開きは小さくなる。
ｃ＜ｄ＜ｂ＜ａ
エ
*ア・イ選択者がそれぞれ27.7％、ウ選択者が16.6％だった。

（２）①　88.9％

10マスで１周期。
６行目１列目は30。

②　46.6％
３列目の数字を拾うと【３、８、13、18、23…】
初項３、公差５の等差数列。
３＋５（ｎ－１）＝５ｎ－２

（３）　21.7％！

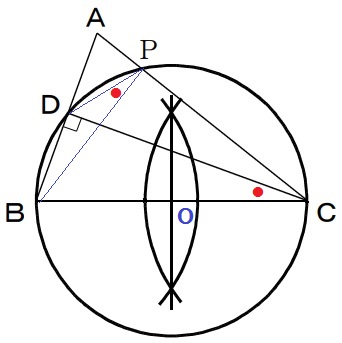
∠ＢＣＤ＝∠ＢＰＤとなるような、辺ＣＡ上のＰを作図する。
弧ＢＤに対する円周角を考える。
Ｂ・Ｃ・Ｄ・Ｐは同一円周上にある→円の作図を試みる。
半円の弧に対する円周角は直角だから、∠ＢＤＣ＝90°
直角三角形ＢＣＤの斜辺ＢＣが円の直径にあたり、その中点が円の中心Ｏである。
①ＢＣの垂直二等分線→交点が中心Ｏ
②円の作図。ＡＣとの交点がＰ。

（４）ｱｲ…50.4％、ｳｴ…62.7％

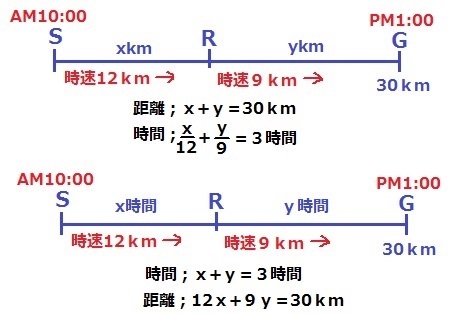
混乱したら図を描いてみよう。
速さがわかっているので、距離と時間で等式を立てる。
ア…30、イ…ｘ/12＋ｙ/９、ウ…３、エ…12ｘ＋９ｙ

大問３（平面図形）

（１）　56.2％
三角形と比の定理。
共通角＋ＤＥ//ＢＣの同位角＝２角相等→△ＡＢＣ∽△ＡＤＥ

（２）①　38.5％
四角形ＥＦＧＨが平行四辺形である証明。

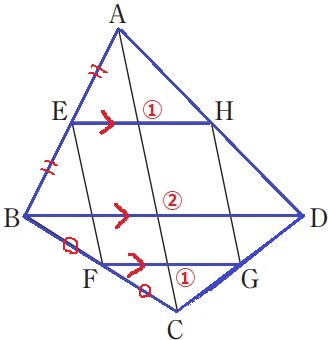
ＡＥ＝ＥＢ、ＢＦ＝ＦＣ
中点連結定理より、ＥＨ：ＢＤ＝ＦＧ：ＢＤ＝①：②
ＥＨ＝ＦＧ＝①
ＥＨ//ＢＤ//ＦＧだから、ＥＨ//ＦＧ
１組の対辺が平行で、かつ長さが等しく、四角形ＥＦＧＨは平行四辺形である。

②　33.5％
菱形は４辺の長さが等しい。

ＥＨとＦＧの長さはＢＤによって決まる。
ＥＦとＨＧの長さはＡＣによって決まる。
ＡＣ＝ＢＤであれば、ＥＦ＝ＦＧ＝ＧＨ＝ＨＥとなる。
エ
*イ選択者が32.5％、ウ選択者が14.9％だった。

（３）　15.4％！

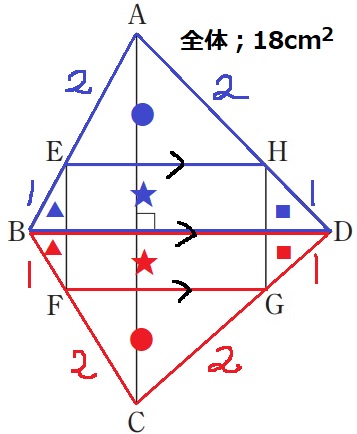
長方形ＥＦＧＨの面積★★を求めたい。
△ＡＢＤと△ＣＢＤの面積は等しいとは限らないが、●▲★■の比の関係は同じ。

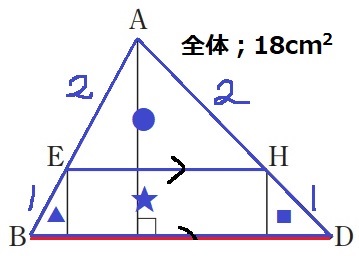
四角形ＡＢＣＤを●●▲▲★★■■に分けたうちの★★は、
△ＡＢＤを●▲★■に分けたうちの★と割合が一緒。
△ＡＢＤの面積を18ｃｍ²と仮定したときの★を求めればいい。

△ＡＥＨ…②×【２】＝④
△ＡＢＤ…③×【３】＝⑨
四角形ＥＢＤＨの面積比…⑨－④＝⑤

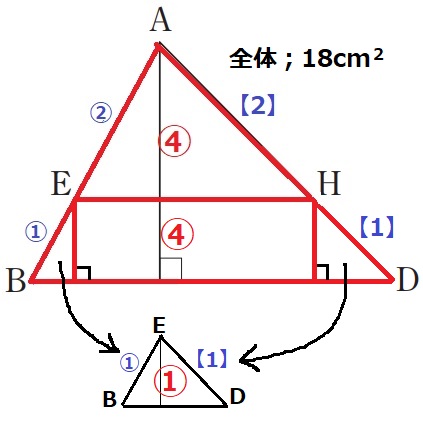
直角を頼りに、両サイドの三角形を合わせる。
△ＥＢＤ…①×【１】＝①
求めたい長方形の面積比は、⑤－①＝④
18×④/⑨＝８ｃｍ²

大問４（確率・整数）

（１）①　66.2％
全体→５×５＝25通り
ｘ＞ｙとなる（ｘ、ｙ）の組み合わせを調べる。
ｘ＝５のとき、ｙは４通り
ｘ＝４のとき、ｙは３通り
ｘ＝３のとき、ｙは２通り
ｘ＝２のとき、ｙは１通り
１＋２＋３＋４＝10通り
確率は、10/25＝２/５

＠別解＠
ｘ＝ｙとなる確率は１/５。
（１回目に”何か”を出す。２回目にその”何か”が出るのは１/５）
ｘ＞ｙとｘ＜ｙは、それぞれ同じ確率になる。
（１－１/５）÷２＝２/５

②　58.2％
今度は同時に２個取り出す。
全体…₅Ｃ₂＝10通り
【少なくとも１個は偶数＝全体－２つとも奇数】
２つとも奇数…３つの奇数から２つをとる。₃Ｃ₂＝３通り
少なくとも１個は偶数…10－３＝７通り
確率は７/10

（２）　30.5％！
100ａ＋10ｂ＋ｃ－（ａ＋ｂ＋ｃ）
＝99ａ＋９ｂ
＝９（11ａ＋ｂ）
11ａ＋ｂは整数だから、９（11ａ＋ｂ）は９の倍数である。

大問５－Ⅰ（関数）

Ⅰ（１）　45.0％

Ｂから垂線、ｘ軸との交点をＤとする。
ＡＤ＝８－２＝６ｃｍ
△ＡＢＤで三平方→ＡＢ＝３√５ｃｍ

（２）　40.6％
答案では求める過程も記述する。
Ｂ（２、３）⇒Ａ（８、０）
右に６、下に３だから、傾きは－３/６＝－１/２
Ｂから左に２、上に１移動して、切片は３＋１＝４
ｙ＝－１/２ｘ＋４

（３）　4.4％!!

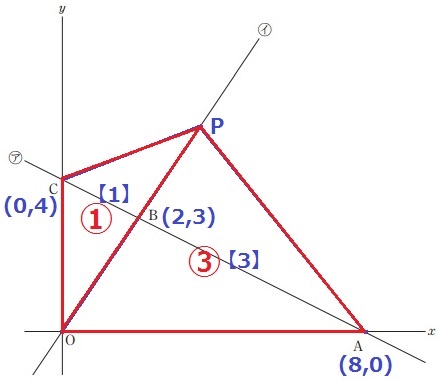
ＣＢ：ＢＡ＝２：６＝【１】：【３】
△ＣＯＰと△ＡＯＰは底辺ＯＰを共通とするので、
面積比は高さの比にあたるＣＢ：ＢＡ＝①：③

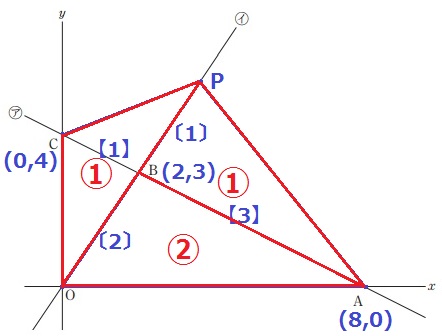
△ＢＡＰは△ＣＯＰと等積だから面積は①。
△ＢＡＯ＝③－①＝②
△ＢＡＯ：△ＢＡＰ＝ＯＢ：ＢＰ＝〔２〕：〔１〕
Ｐのｘ座標は、２×３/２＝３

大問５－Ⅱ（関数）

（１）　61.1％
答案では求める過程も記述する。
Ｃはｙ＝３ｘ－５とｘ軸との交点→ｙ＝０を代入。
０＝３ｘ－５
ｘ＝５/３
Ｃ（５/３、０）

Ｂ（０、３）⇒Ｃ（５/３、０）
傾きは、（０－３）÷（５/３－０）＝－９/５
切片はＢのｙ座標だから、ｙ＝－９/５ｘ＋３

（２）①　8.7％!!
ＢＤ＝ＰＤ＝３－（－５）＝８

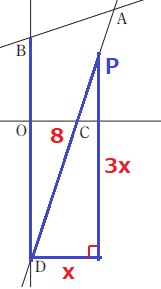
ＰＤを斜辺とする直角三角形で三平方の定理。
直線（イ）の傾きが３なので、横をｘとすると縦は３ｘ。
ｘ²＋（３ｘ）²＝８²
10ｘ²＝64
ｘ＞０、ｘ＝４√10/５

②　0.0％!!!

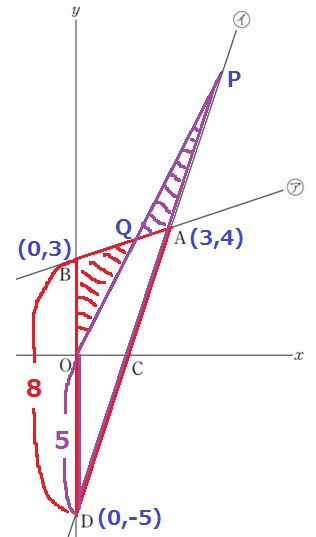
ポイントは他とくっつける。
四角形ＡＱＯＤをつっつけると、△ＡＢＤと△ＰＯＤの面積が等しい。
底辺はＢＤ：ＯＤ＝８：５だから、高さは逆比で５：８。
（ｙ軸～Ａ、ｙ軸～Ｐの距離が５：８になる）
Ｐのｘ座標は、３×８/５＝24/５