2021年度　新潟県公立高校入試問題過去問【数学】解説

平均53.7点（前年比；＋8.4点）

問題はコチラ→ＰＤＦファイル
出題範囲の除外は標本調査。

大問１（小問集合）－85.9％

（１）　99.0％
６－13
＝－７

（２）　93.8％
２（３ａ＋ｂ）－（ａ＋４ｂ）
＝６ａ＋２ｂ－ａ－４ｂ
＝５ａ－２ｂ

（３）　94.8％
ａ³ｂ⁵÷ａｂ²
＝ａ²ｂ³

（４）　92.4％
√14×√２＋√７
＝２√７＋√７
＝３√７

（５）　85.2％
ｘ²＋７ｘ＋５＝０
解の公式を適用。
ｘ＝（－７±√29）/２

（６）　73.3％
ｙ＝ａｘ²に（ｘ、ｙ）＝（－２、12）を代入。
12＝４ａ
ａ＝３
ｙ＝３ｘ²
*ｙ＝－６ｘの誤答が見られた。（比例ではない）

（７）　66.1％

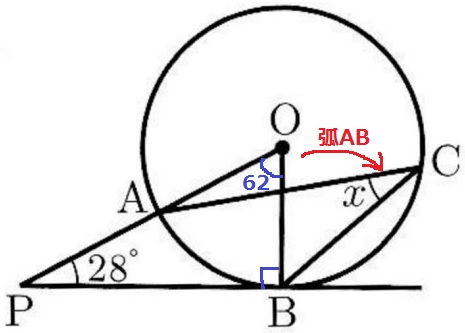
半径ＯＢ⊥接線ＰＢ
直角三角形ＯＢＰの内角で、∠ＰＯＢ＝180－（28＋90）＝62°
これは弧ＡＢに対する中心角で、ｘはその円周角に相当する。
ｘ＝62÷２＝31°

（８）①　77.8％
相対度数は小数であらわす場合が多い。
20÷80＝0.25

②　87.0％
80人の中央値（メジアン）は40番目と41番目の平均。
いずれも600ｍ以上800ｍ未満の階級に属する。
*400ｍ以上600ｍ未満の誤答が見られた。

大問２（小問集合２）－52.2％

（１）　54.2％
答案では求め方も記述する。
連続する２つの自然数をｎ、ｎ＋１とする。
ｎ（ｎ＋１）＝ｎ＋（ｎ＋１）＋55
ｎ²－ｎ－56
＝（ｎ－８）（ｎ＋７）＝０
ｎ＞０だから、ｎ＝８
ｎ＋１＝９
連続する２つの自然数は８と９。
*検算すると、（８＋９）＋55＝72＝８×９
誤答では７、８が見られた。

（２）　67.8％
答案では求め方も記述する。
異色より同色を出すパターンの方が少ない。
【全体－同色＝異色】
全体は５×３＝15通り
■赤２個
Ａから赤、Ｂから赤₁か赤₂⇒２通り
■白２個
Ａから白₁か白₂、Ｂから白⇒２通り
同色２個は計４通り。
異色２個は15－４＝11通り
確率は11/15

（３）　31.2％！

適当なＤを描いてみる。
△ＡＢＤの内角で、∠ＢＡＤ＝180－（60＋105）＝15°

これみよがしにＭが与えられているので、
ＡＭに線をひいて正三角形ＡＢＣを真っ二つに割ると∠ＢＡＭ＝30°だから、
∠ＤＡＭ＝30－15＝15°
ということは、ＡＤは∠ＢＡＭの二等分線である。
これとＢＣとの交点がＤとなる。
*誤答ではＤをＢＭの中点とするものが見られた。

大問３（数量変化）－33.1％

（１）　68.3％
原点から右に６、上に180なので、
直線の傾きは180÷60＝30
*誤答では傾きではなく、方程式を書くものが見られた。
問題文をよく読もう！

（２）①　37.0％

グラフ上で相似図形をつくる。
？＝50×６/４＝75
切片ｂ＝180－75＝105
*誤答ではｂ＝180が見られた。

②　21.7％！

折れ曲がったあとの線はＰだけ。
これをｙ軸に延長した青線の上昇分、230－105＝125ＬはＰだけの場合。
230Ｌのうち、Ｐからは125Ｌ、Ｑからは105Ｌの水が出た。
青線Ｐを原点に移すとうえのようになる。
エ

（３）　14.7％！
答案では求め方も記述する。
Ｐは10分で125Ｌ出す。
Ｑは105Ｌ出す。Ｐが105Ｌとなるのは、
10×105/125＝８・２/５分＝８分24秒後

大問４（平面図形）－26.1％

（１）　31.8％！

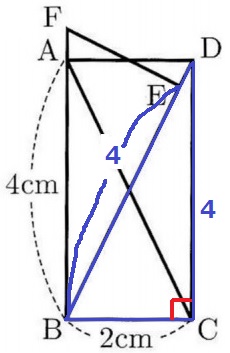
【ＤＥ＝ＤＢ－ＥＢ】
△ＢＣＤで三平方→ＤＢ＝２√５ｃｍ
△ＡＣＤ≡△ＦＢＥより、ＥＢ＝ＤＣ＝４ｃｍ
ＤＥ＝２√５－４ｃｍ

（２）①　87.4％
素直にリード文に従う。

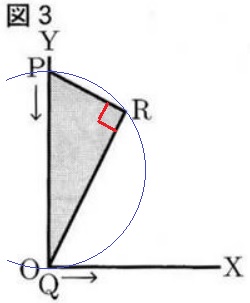
∠ＱＲＰ＝∠ＢＥＦ＝∠ＤＣＢ＝90°

②　68.4％
上図のように３点Ｐ、Ｑ、Ｒを通る円を描く。
半円の弧に対する円周角ＰＲＱは90°
直径はＰＱ。

③　5.9％!!

リエの考え方『３点Ｐ、Ｑ、Ｒを通る円』を描いてみる。
∠ＰＯＱ＝90°ゆえ、Oは直径をＰＱとする円周上にあり、
４点Ｏ、Ｐ、Ｒ、Ｑは同一円周上にあることになる。
弧ＲＱに対する円周角より、∠ＲＯＸ＝∠ＲＰＱとなる。
*誤答では、４点ＯＰＱＲが同一円周上にあることを既知として証明するものがみられた。

④　0.4％!!!
答案では求め方も記述する。

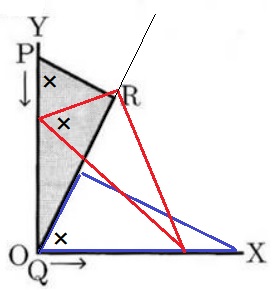
一応、Ｒが一直線上を動く理由を確認しておくと、
前問の∠ＲＯＸ＝∠ＲＰＱの証明より、∠ＲＰＱの大きさは変わらないので、
∠ＲＯＸの大きさも変わらない→Ｒは１つの直線上を動く。
…なんとなくＲがいったん上へ戻ってそう。

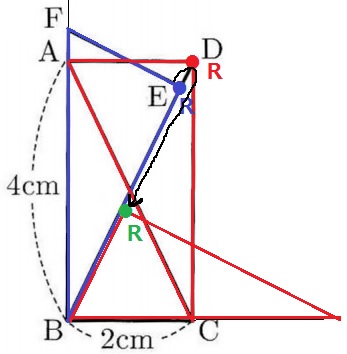
図１に立ち返るとＲの軌跡が見えやすいと思う。
ＲがＢ（Ｏの位置）から最も離れるのはＤにいるとき。
【Ｅ⇒Ｄ⇒Ｒ】の順に動く。

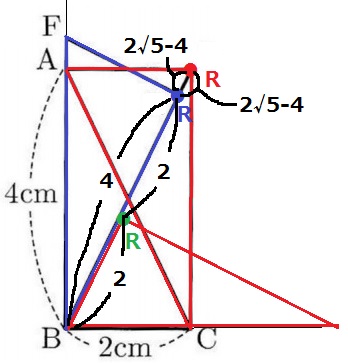
（１）の数字を使う。
（２√５－４）×２＋（４－２）
＝４√５－６ｃｍ

大問５（空間図形）－44.7％

（１）　87.9％
ＭとＮはそれぞれ中点→中点連結定理を適用。
ＭＮ＝ＣＤ÷２＝８÷２＝４ｃｍ

（２）　44.9％
△ＡＥＭ∽△ＢＦＥの証明。

数値が与えられている場合はそれを用いる。
ＡＥ＝２ｃｍ、ＡＭ＝４ｃｍ
ＢＦ＝３ｃｍ、ＢＥ＝６ｃｍ
ＡＥ：ＢＦ＝ＡＭ：ＢＥ＝２：３
正三角形ＡＢＣの内角より、∠ＭＡＥ＝∠ＥＢＦ＝60°
２辺の比とあいだの角が等しいので∽。
*誤答では、２つの三角形が直角三角形であることを既知として利用したものが見られた。

（３）　1.5％!!
答案では求め方も記述する。

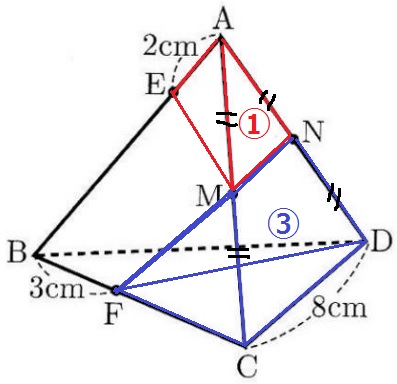
底面積の比はわかりやすい。
△ＡＭＮ∽△ＡＣＤより、△ＡＭＮ：四角形ＭＣＤＮ＝①：③
あとは高さの比さえわかれば体積比がでる。

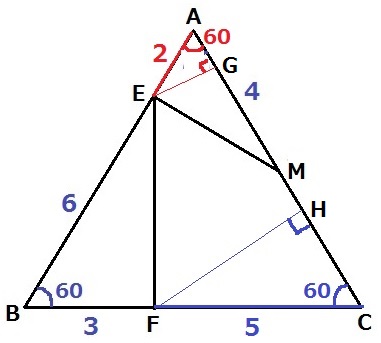
前問の図を手がかりにする。
ＥとＦから垂線をひき、ＡＣとの交点をＧ、Ｈとすると、
三角錘Ｅ―ＡＭＮと四角錘ＦーＭＣＤＮの高さはＥＧ、ＦＨにあたる。

△ＡＥＧと△ＣＦＨは内角が30°－60°－90°の直角三角形で相似。
三角錘Ｅ―ＡＭＮと四角錘ＦーＭＣＤＮの高さの比はＥＡ：ＦＣに相当する。
ＥＡ：ＦＣ＝【２】：【５】
三角錐Ｅ―ＡＭＮ：四角錐ＦーＭＣＤＮ
＝①×【２】：③×【５】
＝２：15
四角形ＦーＭＣＤＮの体積は、三角錘Ｅ―ＡＭＮの15/２倍。