2016年度　千葉県公立高校入試【後期】数学解説

平均５７．９点
問題はコチラから→ＰＤＦファイル

大問１（計算）－89.7％

（１）　99.0％
８－１５
＝－７

（２）　97.2％
３＋（－４）²÷８
＝３＋１６÷８
＝３＋２
＝５

（３）　85.1％
３(１/２ｘ－２/３ｙ)－１/２ｘ－ｙ
＝３/２x－２ｙ－１/２ｘ－ｙ
＝ｘ－３ｙ

（４）　90.2％
連立方程式
ｘ－２ｙ＝－８　・・①
３ｘ＋ｙ＝１１　・・②
　
加減法でも代入法でも。以下、代入法。
①から、ｘ＝２ｙ－８
②に代入
３（２ｙ－８）＋ｙ＝１１
ｙ＝５
②に放り込む
３ｘ＋５＝１１
ｘ＝２　　ｙ＝５

（５）　85.1％
－√７５＋１２/√３
＝－５√３＋４√３
＝－√３

（６）　81.8％
２ｘ²－３ｘ－１＝０を解きなさい。
因数分解できないので、素直に解の公式。
ｘ＝３±√９＋８/４
＝３±√１７/４

大問２（小問集合）－63.8％

（１）　93.0％
空間認識。立面図は正面から、平面図は上から立体をみている。
ア→立方体、イ→三角柱、ウ→四角錘、エ→三角錐
よって、ウ。

（２）　69.0％
得点×度数の合計が総得点。総得点÷人数＝平均
５×２＋４×７＋３×５＋２×４＋１×１＋０×１＝６２点・・総得点
６２÷２０＝62/20＝31/10＝3.1
今年の度数分布表は基本であった。

（３）　54.6％
いずれも座標が不明。正方形の特徴から考える。
正方形の面積は〔対角線×対角線÷２〕
ＡＢ×ＣＯ÷２＝８
ＡＢ＝ＣＯ＝４
正方形の対角線は直角に交わり、中点を通る。
Ｂ（２、２）から、２＝２²ａ　　ａ＝１/２

（４）　75.3％
２ａ＋ｂが３の倍数。
ａを基準に組み合わせを考える。
（ａ、ｂ）＝（１、１）（１、４）（２、２）（２、５）（３、３）（３、６）（４、１）（４、４）（５、２）（５、５）（６、３）（６、６）
*面倒くさいが、ｂは〔ａ＋３〕すれば少し楽。
よって、１２/３６＝１/３

（５）　27.2％！
７５°を作成する。前期と比べたら易しめ。
作図できる９０、４５、６０、３０をうまく活用して、和を７５にすればいい。
以下、７５＝６０＋１５＝６０＋（３０÷２）のやり方（公式解答２番目）

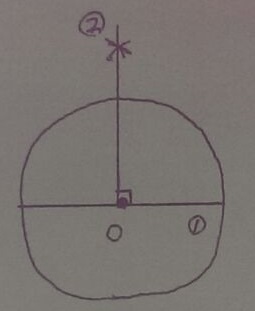
適当な直径をひく。モンスターボールみたい。

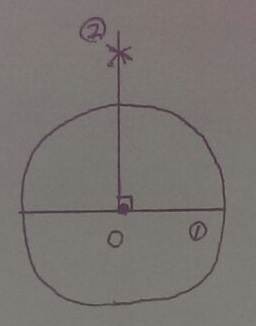
直径の両端から適当な長さをとる。
直径の垂直二等分線。

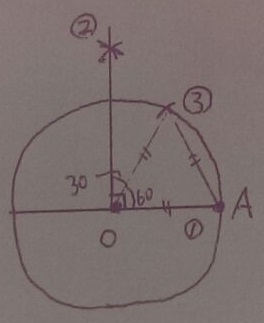
直径の右端をAとする。Aから半径の長さをとる。
正三角形が出現。直角を３０°と６０°に分ける。
３０を二等分し、１５と６０をたせば７５になる。

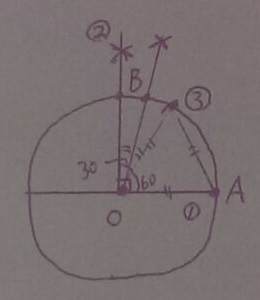
↑④角の二等分線
文字A、Bを書き忘れないように。

*公式解答１番目のやり方は、７５＝４５＋３０＝９０÷２＋（９０－６０）
直径の垂直二等分線をひき、左を直角の二等分線、右を正三角形、その間が７５となる。

大問３（図形の移動）－32.0％

（１）　49.9％
３ｃｍまでは縦ｘｃｍ、横ｘｃｍの直角二等辺三角形。
ｙ＝ｘ×ｘ×１/２
y＝１/２ｘ²

（２）①　41.1％
ｙの最大値Мは点Cが点Fと重なったとき。
３＜ｘ≦６は台形になる。

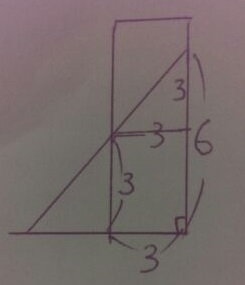
ＥＦに平行な線をひくと、上にも直角二等辺があらわれる。
（３＋６）×３×１/２=２７/２cm²

②　4.9％!!
Ｍ＝２７/２
ｘ＝３のとき、３×３×１/２＝９/２cm
Ｍの半分に満たない→３＜ｘ＜６、Ｍ/２は台形のとき。

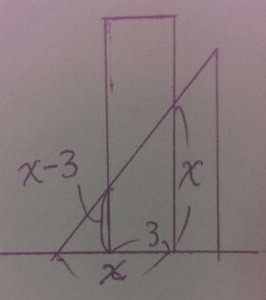
↑求めたいところをｘとおくとこんな感じに。
前問の通り、左の辺は右の辺（ｘ）の－３。
あとは台形の公式にのせるだけ。
（ｘ－３＋ｘ）×３×１/２＝２７/２×１/２
３（２ｘ－３）＝２７/２
２ｘ－３＝９/２
ｘ＝１５/４

*２次方程式ではなかった。
大問４からキツくなるので、ここまでは快速でいきたい。

大問４（平面図形）－47.8％

（１）
前期と比べると、やや難しくなっている。
誘導に従う。
（ａ）…選択肢のなかから、正三角形の１つの角を選ぶ。ア　95.7％
（ｂ）…角度の話しかしていませんからね。オ　　　　　　　90.2％
（ｃ）６点―3.4％！　３点―2.8％　無答―57.9％！
△ＥＣＦと△ＡＧＣをみつめる。
正三角形が３つあるので、等しい辺に記号をふる。
また、④（平行四辺形の対辺は等しい）とあわせると２辺が等しいことがわかる。
すなわち、２辺の間の角である∠ＥＦＣ＝∠ＡＣＧがわかれば嬉しい。
⑤で∠ＢＣＦ＝∠ＥＦＣ（錯角）の誘導が残されているので、
∠ＢＣＦ＝∠ＡＣＧの証明さえ整えれば、全て説明がつく。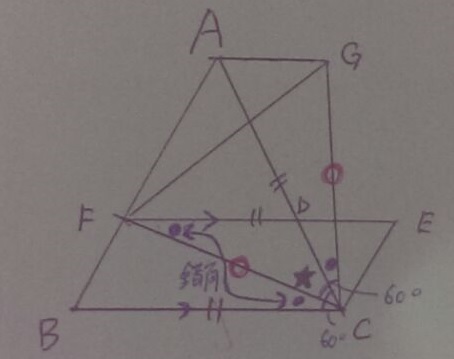
∠ＢＣＦ＝∠ＡＣＢ－∠ＡＣＦ＝６０－★
∠ＡＣＧ＝∠ＧＣＦ－∠ＡＣＦ＝６０－★
正三角形の内角と、共通する∠ＡＣＦをひくと同じ角度になる。
ここさえ丁寧に記述できれば、６点ゲットも間近。

以下、公式解答引用
―――引用はじめ―――
△ＥＣＦと△ＡＧＣにおいて、
△ＡＢＣは正三角形であるから、
ＢＣ＝ＡＣ　…⑥
④、⑥より、　ＥＦ＝ＡＣ　…⑦
△ＧＣＦは正三角形であるから、
ＣＦ＝ＧＣ　…⑧
∠ＡＣＢ＝∠ＧＣＦ＝６０°より、
∠ＡＣＧ＝６０°－∠ＡＣＦ
∠ＢＣＦ＝６０°－∠ＡＣＦ
したがって、∠ＢＣＦ＝∠ＡＣＧ　…⑨
⑤、⑨より、∠ＥＦＣ＝∠ＡＣＧ　…⑩
⑦、⑧、⑩より、２辺とその間の角がそれぞれ等しいので、
△ＥＣＦ≡△ＡＧＣ
―――引用おわり―――

（２）　1.8％!!
悩みどころ。
図形がごちゃごちゃしているので、的確な方針がないと迷ってばかりになる。
△ＣＥＨと△ＢＦＣは互いに位置が離れているが、
四角形ＦＢＣＥが平行四辺形なので高さが等しい。
つまり、底辺であるＨＥ：ＢＣ＝△ＣＥＨ：△ＢＦＣとなる。
ＢＣは正三角形の１辺で５。
では、ＨＥの長さはいくつだろうか？
ＤＥが正三角形の１辺なので２。
ＤＨが知りたい。
中途半端な場所にあるが△ＡＣＧ をみると…なんとなくＡＧがＤＨと平行にみえる。

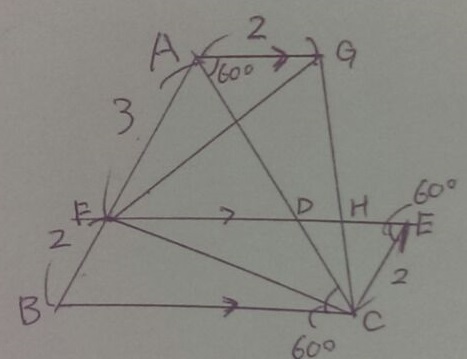
正三角形の内角と、前問の合同で６０°の位置を確認。
すると、∠ＧＡＣ＝∠ＡＣＢ（錯角）→ＡＧ//ＢＣ
平行四辺形と組み合わせれば、ＡＧ//ＦＥ//ＢＣ

３本の平行線が見つけられるかどうかが成否の分水嶺(ぶんすいれい)。
平行線の線分の比を駆使する。

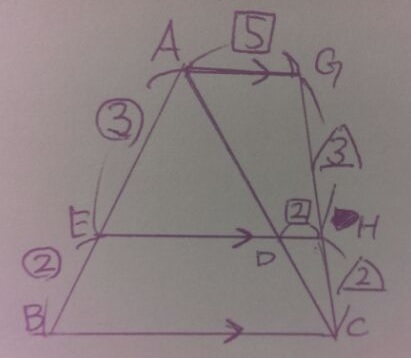
↑余分な線分をカット。
△ＣＧＡ∽ＣＨＤから、ＡＧ：ＤＨ＝５：２
ＡＧ＝２、ＤＨ＝２×２/５＝４/５

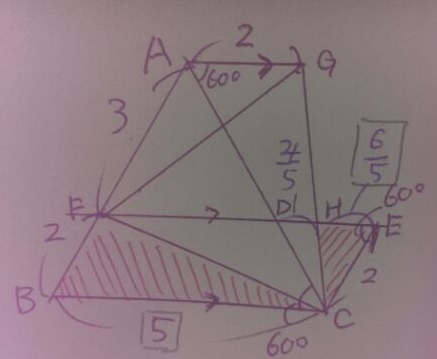
図がモヤ～となってしまった(-_-;)
ＨＥ＝２－４/５＝６/５
したがって、△ＣＥＨ：△ＢＦＣ＝ＨＥ：ＢＣ＝６/５：５＝６：２５
*ＡＧがなんとなく平行線にみえるかどうか。
根拠なくして証明をしてはならないが、指針を立てるうえでは感覚も大切。

大問５（規則）－33.6％

点の位置が反時計回りに、ピ、ピ、ピ、ピョーンと移動する。
（１）　78.1％
（０、１）からスタートし、左→下→右→上と移動する。
４の倍数ごとに方位がかわる。
１４秒後は、１４÷４＝３・・２
整理すれば、１４＝２＋４×３
つまり、スタートから２進み、そこから３周まわったところ。
スタートから２進むと（０、－１）
ここから３周なので、１４秒後の点Ｐは下に３つ。
よって、Ｐ（０、－４）

（２）　43.0％
（－１５、０）ということは左方向。
１秒後に（－１、０）、４秒ごとに１周して（－２、０）（－３、０）・・。
左方向に点Ｐがくる秒数を数列にあらわすと、
１秒後、５秒後、９秒後、１３秒後、１７秒後・・・
上の数列の１５番目が答え。あとは、数列の基本問題。
１＋４×（１５－１）＝５７秒後

（３）　12.2％！
前問の状態から点Ｐを移動させる。
「ｍは４の倍数 」なので、（－１５、０）を出発してから４の倍数後のみを考える。
言い換えれば、１周してまた左方向に戻ってくるので、
（－１５、０）の左側に点Ｐがあらわれることになる。
（－１５、０）から４秒後に（－１６、０）
その４秒後に（－１７、０）、４秒後（－１８、０）･･･
ｘ軸方向に－１、すなわち－ｍ/４ずつ移動する（ｍは４の倍数の秒なので÷４）。
よって、（－１５、０）から移動を始めてから（－１５－ｍ/４、０）

（４）　1.1％!!
Ｂがｙ軸上にある→Ｂは上方向か下方向。
まずは、Ｂの位置を確定する。

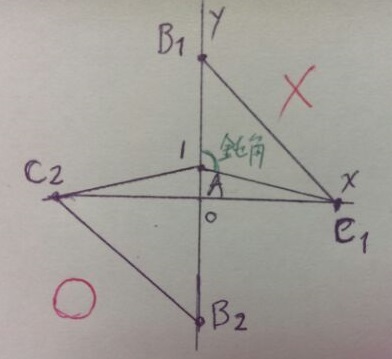
実際に描いて見る。
Ｂから３秒後がＣなので、ＣはＢから反時計回りに２７０度回転した場所にくる。
Ｂが上方向にくると、∠ＢＡＣが鈍角になってしまう。
△ＡＢＣは鋭角三角形なので不適。
したがって、Ｂは下方向にくる。

Ｂから原点までの距離をｄとおく。
ＡＢはｄ＋１
ＣＯの距離は、上方向にくると原点までの距離が＋１されるのでｄ＋１となる。
△ＡＢＣの面積は、
（ｄ＋１）×（ｄ＋１）×１/２＝７２
（ｄ＋１）²  ＝１４４
ｄ² ＋２ｄ＋１＝１４４
ｄ² ＋２ｄ－１４３
＝（ｄ＋１３）（ｄ－１１）＝０（*１３×１１＝１４３）
ｄは距離ゆえにｄ＞０、ｄ＝１１
Ｂ（０、－１１）
あとは、（２）と同様に考える。
下方向の秒数を数列であらわすと、
２、６、１０、１４、１８、２２・・
１１番目は、２＋４×（１１－１）＝４２（秒後）

座標から規則をつかみ、数列に置き換えれば対処しやすいかもしれない。
公立高校入試解説ページに戻る