平均54.3点（前年比；＋1.1点）
問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１）
９＋２×（－３）
＝９－６
＝３
（２）
３ｘ2ｙ×４ｙ2÷６ｘｙ
＝２ｘｙ2
（３）
９/√３－√48
＝３√３－４√３
＝－√３
（４）
３（３ａ＋ｂ）－２（４ａ－３ｂ）
＝９ａ＋３ｂ－８ａ＋６ｂ
＝ａ＋９ｂ
（５）
２ｘ＋５ｙ＝－２ …①
３ｘ－２ｙ＝16 …②
①×３－②×２をすると、19ｙ＝－38
ｙ＝－２
②に代入、３ｘ＋４＝16
ｘ＝４
ｘ＝４、ｙ＝－２
（６）
（ｘ－２）2＝25
ｘ－２＝±５
ｘ＝２±５
ｘ＝－３、７
（７）
全部でチョコはａ個。
配った個数は８ｂ個、余りが５個。
ａ＝８ｂ＋５
（８）
全体は６×６＝36通り
差が３になる⇒ＡーＢ＝３、Ｂ－Ａ＝３どちらでもＯＫ。
（１、４）（２、５）（３、６）とこれらの逆を含めて６通り。
確率は６/36＝１/６
（９）
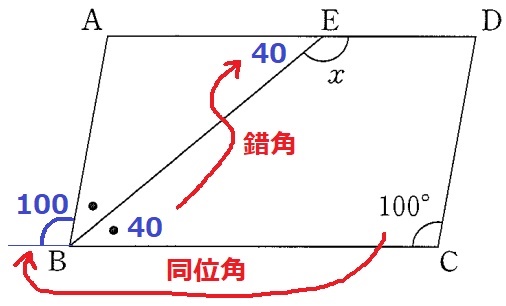
同位角で100°を移す。
∠ＥＢＣ＝（180－100）÷２＝40°
錯角で40°を移し、ｘ＝180－40＝140°
（10）
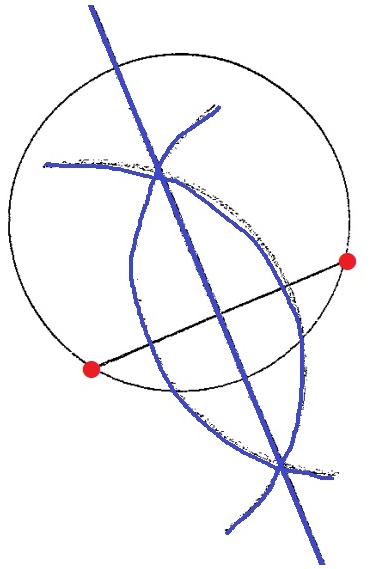
円の対称の軸→円の中心を通る直線。
適当な円周上の２点の垂直二等分線をひけばいい。
大問２（関数）
（１）
ｙ＝１/２ｘ2は下に凸のグラフで、－１≦ｘ≦２は原点を通る。
ｘ＝０のとき、最小値ｙ＝０
ｘ＝２のとき、最大値ｙ＝２
０≦ｙ≦２
（２）
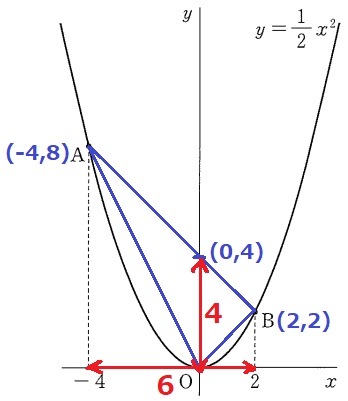
ｙ＝１/２ｘ2に代入して座標を求める。
Ａ（－４、８）→Ｂ（２、２）
右に６、下に６だから、傾きは－６/６＝－１
ＡＢの切片は、Ｂから左に２、上に２移動して２＋２＝４
△ＯＡＢの面積は、４×６÷２＝12
（３）
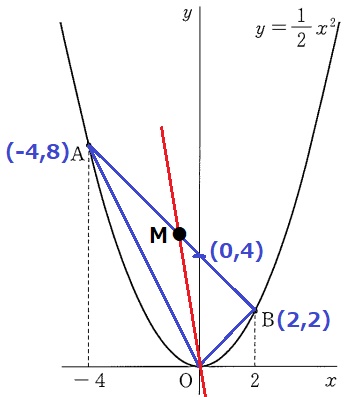
Ｏを通り、△ＯＡＢを２等分する直線→ＯとＡＢの中点を通る直線。
中点をＭとする。Mのｘ座標は、（－４＋２）÷２＝－１
ｙ座標は、（８＋２）÷２＝５
M（－１、５）→原点Ｏ
右に１、下に５、傾きは－５。
ｙ＝－５ｘ
大問３（データの活用）
（１）
３/25＝12/100＝0.12
（２）
25人の中央値は、（25＋１）÷２＝13番目の値。
これは15日以上20日未満の階級に含まれる。
（３）
ア：Ｑ組の15日以上は、８＋８＋５＝21人いる。〇
イ：最頻値（モード）は最もあらわれている値。
Ｐ組は15～20日の階級→17.5日、Ｑ組は10～15日→12.5日×
ウ：Ｐ組―５/25＝１/５、Ｑ組―８/40＝１/５〇
エ：最大値はともに25～30日の階級に含まれるが、何人いるか詳細はわからない。×
オ：Ｐ組―（３＋３）/25=６/25、Ｑ組―（２＋５）/40＝７/40
分子は１しか違う。分母がそれ以上に小さいＰ組の方が値は大きい。〇
ア・ウ・オ
大問４（規則）
（１）
【１、３、６、10…】
＋２、＋３、＋４…→６番目は１～６の和。
（１＋６）×６÷２＝21
（２）
【６、12、18…】
ｎ番目は６ｎ。
＠余談＠
図形の周の長さは、長方形の周囲と同じ。
（３）
等差数列の和の公式を覚えておく！
ｎ番目のタイルの枚数…１～ｎまでの和→ｎ（ｎ＋１）/２
ｎ番目の周の長さ…６ｎ
ｎ（ｎ＋１）/２＝６ｎ ←両辺２倍
ｎ（ｎ＋１）＝12ｎ
ｎ2－11ｎ
＝ｎ（ｎ－11）＝０
ｎ＞０だから、ｎ＝11
11番目の周の長さは、６×11＝66
ウ…11 エ…66
大問５（空間図形）
（１）
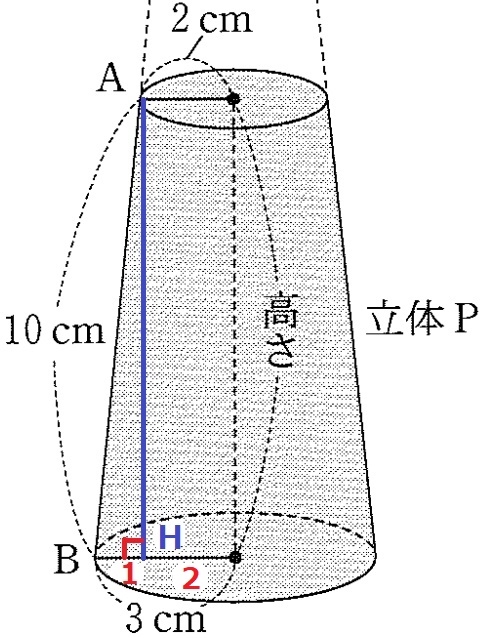
Ａから底面に垂線をひき、足をＨとする。
ＢＨ＝３－２＝１ｃｍ
△ＡＢＨで三平方→高さＡＨ＝３√11ｃｍ
（２）
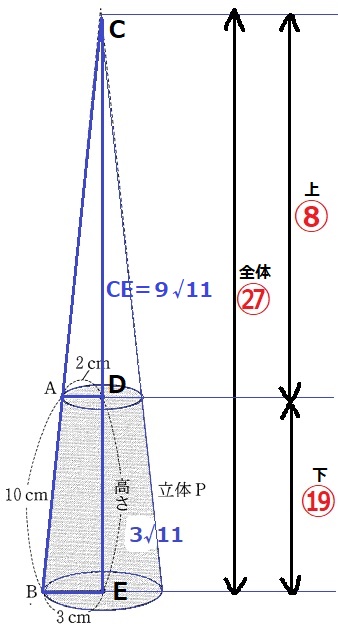
図の点をＣ・Ｄ・Ｅとする。
△ＣＡＤ∽△ＣＢＥの相似比は２：３。
ＣＤ：ＤＥ＝２：１だから、ＣＥ＝３√11×３＝９√11ｃｍ
体積比は相似比の３乗→上の三角錐：全体の三角錐＝２3：３3＝⑧：㉗
下の立体Ｐ（円錐台）の体積比は、㉗－⑧＝⑲
立体Ｐの体積は、３×３×π×９√11÷３×⑲/㉗＝19√11πｃｍ3
（３）
円錐台の赤い円をコロコロ転がしたら、青い円の円周になる。
赤い円の円周…２×２×π＝４πｃｍ
円錐の頂点ＣがＯにあたる。
青い円の半径は△ＣＡＤ∽△ＣＢＥの相似比２：３から、ＣＡ＝10×２＝20ｃｍ
青い円の円周…20×２×π＝40πｃｍ
円錐台が回転した回数は、40π÷４π＝10回
＠公式＠
円錐の回転数＝母線÷半径＝30÷３＝10回
大問６（数量変化）
（１）
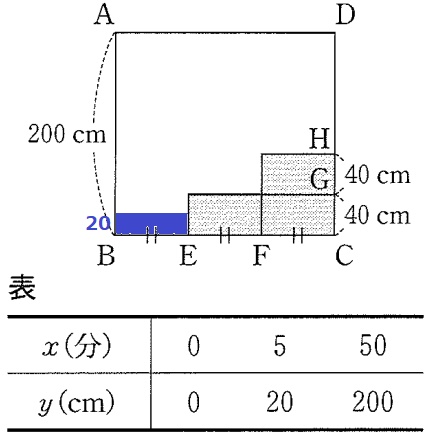
ｘ＝５のとき、ｙ＝20
20ｃｍはまだ段差の影響を受けていない→比例が使える。
ｘ＝１のとき、ｙ＝20×１/５＝４
（２）
側面図が管理しやすい。
20ｃｍで５分だから、40ｃｍは10分かかる。
次の40ｃｍは底面積が２倍になる→体積２倍→時間は２倍かかるから20分間。
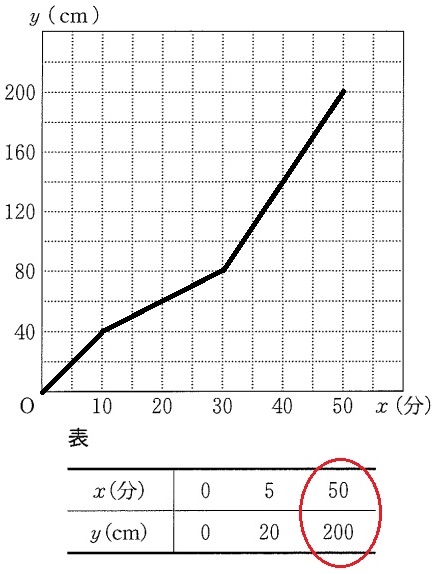
原点から（10、40）、20分後の（30、80）を結ぶ。
高さ80ｃｍから給水口Ⅱが追加されるが、水量はわからない。
表にｘ＝50、ｙ＝200とあるので、（50、200）まで線を引く。
（３）
80≦ｙ≦200の直線で、（30、80）→（50、200）
右に20、上に120だから、傾きは120/20＝６（１分間に６ｃｍ上昇）
（30、80）から20ｃｍ上昇して100ｃｍになる。
20÷６＝３・１/３分＝３分20秒
30分から３分20秒後の33分20秒後。
（４）
満水から水を排出する。
段差が厄介。まずは段差のないＨまで水面が下がる時間を求める。
２段目の段差を１段目に移すと、ちょうど水槽の下40ｃｍが埋まる。
ということは、水の容積は水槽の高さ160ｃｍ分に相当し、これが60分で排出する。
Ｈまで水面が下がる時間は、60×120/160＝45分
Ｈから残り３分間、水を減らす。
45分で120ｃｍの減少。
さらに底面積が２/３倍に減るで、水面の高さの減少スピードは逆比で３/２倍に上がる。
残り３分で水面の高さは、120×３/45×３/２＝12ｃｍ減る。
ＨＣ＝80ｃｍだから、水面の高さは80－12＝68ｃｍ
大問７（平面図形）
（１）
△ＡＣＥ≡△ＢＣＦの証明。
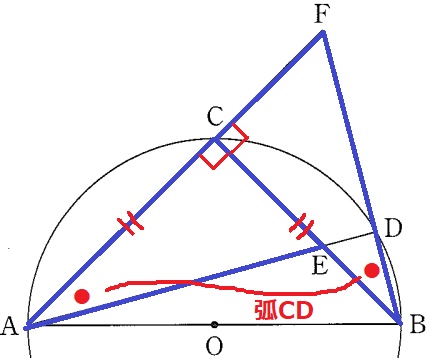
仮定より、ＡＣ＝ＢＣ
直径に対する円周角で、∠ＡＣＥ＝∠ＢＣＦ＝90°
弧ＣＤに対する円周角で、∠ＣＡＥ＝∠ＣＢＦ（●）
１辺と両端角が等しいから△ＡＣＥ≡△ＢＣＦ
（２）
角度の情報が与えられたので角度を調査する。
∠ＡＣＢ＝90°、ＡＣ＝ＢＣより、△ＡＢＣは直角二等辺三角形。
∠ＥＡＢ＝45－15＝30°、∠ＥＢＡ＝45°
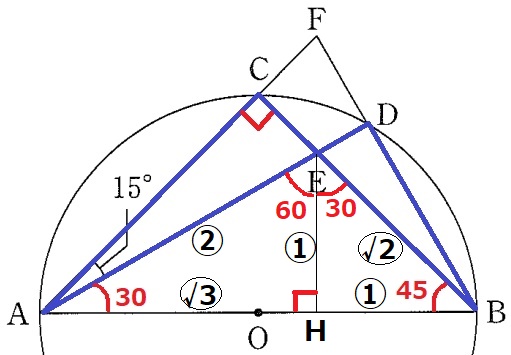
30°も45°も有名三角形の内角。
ＥからＡＢに垂線、足をＨとする。
△ＡＨＥの辺の比は１：２：√３、△ＢＨＥは１：１：√２。
△ＡＣＥと△ＢＤＥは対頂角＋円周角で２角相等の∽。
相似比は対応する辺の比から、ＡＥ：ＢＥ＝２：√２
面積比は相似比の２乗、△ＡＣＥ：△ＢＤＥ＝２2：（√２）2＝２：１
（３）
Ｃは弧ＡＢの真ん中。
半径３ｃｍの４分の１円から直角二等辺ＯＢＣをひくと、
３×３×π×１/４－３×３÷２＝９/４π－９/２ｃｍ2
これから△ＢＤＥをひけばいい。 Ｅに関する比が欲しい。
△ＡＢＦ＝△ＡＢＥ×２ということは、△ＡＢＥ＝四角形ＡＥＢＦ
（１）△ＡＣＥ≡△ＢＣＦだったので、それぞれの面積を★とすると、△ＡＢＥ＝★★
△ＡＣＥ：△ＡＥＢ＝ＣＥ：ＥＢ＝①：②
ＡＣ＝ＢＣ＝③
△ＡＣＥで三平方→ＡＥ＝〇√10
△ＡＣＥ：△ＢＤＥ＝（√10）2：２2＝⑤：②
方針；【△ＡＢＣ→△ＡＣＥ→△ＢＤＥ】
６×３÷２×①/③×②/⑤＝６/５ｃｍ2
したがって、求積すべき図形の面積は、
（９/４π－９/２）－６/５＝９/４π－57/10ｃｍ2
大問１
（６）展開しないで解きたい。
（８）Ａ＞Ｂ、Ａ＜Ｂの２パターンある。
（９）等角●の大きさを優先的に調べる。
（10）もう１つの垂直二等分線を描けば、円の中心点がわかる。
大問２・３
オーソドックスな問題であった。
後半の大問が難しいので、ここは積み上げておきたい。
大問４
（３）等差数列の和の公式は高校受験では原則扱わないようだが、
原理は小学生でもわかるので知っておいた方がいい。
大問５
（３）図２の外側の円でもできる。
大問６
正答率は低そう。
（１）図２と表を照らし合わせて、０～５分後までは比例が使えると判断する。
（２）転換点はｙ＝40と80、底面積２倍で水面上昇のスピードは半分に落ちる。
ｙ≦80の給水口Ⅱも厄介。ⅠとⅡが同じ水量とは限らない。表に戻る。
（４）
やり方次第で解答時間が変わりやすい。
まずはｙ＝80まで水面が減る時間を求める。水を変形すると求めやすい。
底面積の比と水面の変化速度が逆比。
大問５
（２）30°と45°から有名三角形を使って対応する辺の比を求める。
（３）面白い問題だったが、６で時間を費やし過ぎると間に合わない。
面積の条件をどう使うか。△ＡＢＥと四角形ＡＥＢＦが等積。
これに（１）の合同を使うとＣＥ：ＥＢがわかる。面積比の処理もテクがいる。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント