2021年度　東京都立高校入試問題過去問・分割後期【数学】解説

問題はコチラ→ＰＤＦファイル
2021年度・都立（数学）の解説はコチラ。
出題範囲の除外は三平方の定理と標本調査。

大問１（小問集合）

（１）
－３－１/２×６
＝－３－３
＝－６

（２）
（ａ＋７）/４＋（ａ－９）/８
＝｛２（ａ＋７）＋（ａ－９）｝/８
＝（３ａ＋５）/８

（３）
（３√５＋６）（３√５－６）
＝（３√５）²－６²
＝45－36＝９

（４）
２（ｘ＋８）＝７－ｘ
３ｘ＝－９
ｘ＝－３

（５）
５ｘ－３ｙ＝９　…①
ｙ＝ｘ＋１　…②
②を①に代入。
５ｘ－３（ｘ＋１）＝９
ｘ＝６
②に代入。ｙ＝６＋１＝７
ｘ＝６、ｙ＝７

（６）
ｘ²－５ｘ－４＝０
解の公式です。
ｘ＝（５±√41）/２

（７）
33ｋｇ以上は18人。
18/40＝45/100＝45％
あ…４、い…５

（８）

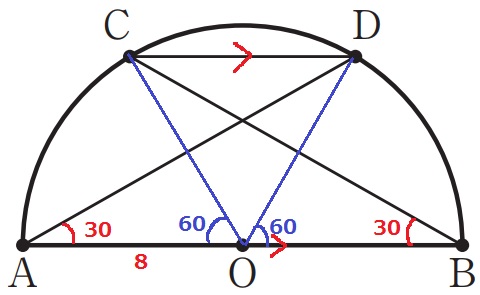
弧ＣＤの長さを求めるには、中心角ＣＯＤが知りたい。
ＯＣ・ＯＤに補助線をひく。

ＡＢ//ＣＤから、全体が左右対称である。
∠ＢＡＤ＝∠ＡＢＣ＝30°
中心角は円周角の２倍。∠ＡＯＣ＝∠ＡＢＣ×２＝60°
同様に、∠ＢＯＤ＝60°
∠ＣＯＤ＝180－（60＋60）＝60°
弧ＣＤの長さは、８×２×π×１/６＝８/３πｃｍ
イ

（９）
△ＡＢＣの外接円の中心を作図する。

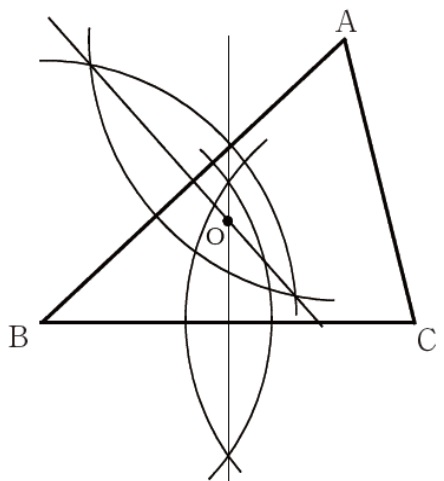
辺ＡＢ・ＢＣ・ＣＡの垂直二等分線のうち、２本の交点がＯとなる。

大問２（式の証明）

（１）
２π（ａ＋１）－２πａ＝２π
ウ

（２）

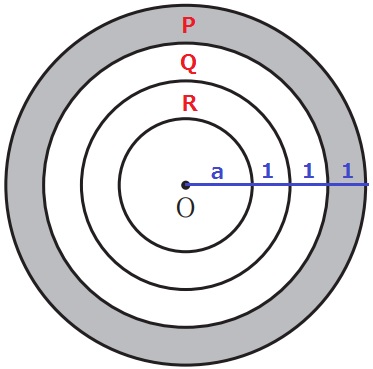
１つずつ面積を求めていく。
Ｐ＝π（ａ＋３）²－π（ａ＋２）²＝２πａ＋５π
Ｑ＝π（ａ＋２）²－π（ａ＋１）²＝２πａ＋３π
Ｒ＝π（ａ＋１）²－πａ²＝２πａ＋π

Ｐ－Ｑ＝（２πａ＋５π）－（２πａ＋３π）＝２π
Ｑ－Ｒ＝（２πａ＋３π）－（２πａ＋π）＝２π
Ｐ－Ｑ＝Ｑ－Ｒ＝２πで題意は示された。

大問３（関数）

（１）
ｙ＝１/４ｘ²において、
ｘ＝０のとき、最小値ｙ＝０
ｘ＝－４のとき、最大値ｙ＝４
０≦ｂ≦４
①…エ、②…キ

（２）
Ａ（－４、０）→Ｐ（４、４）
右に８、上に４なので、傾きは１/２。
Ａから右に４、上に２移動して、切片は２。
ｙ＝１/２ｘ＋２
①…ウ、②…ア

（３）

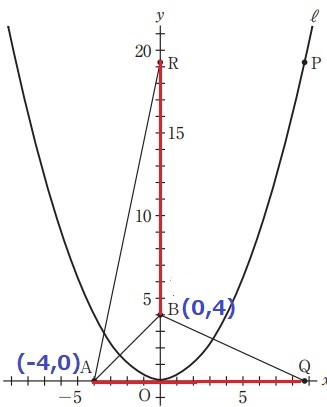
面積が等しい△ＡＢＲと△ＡＢＱの高さはともに４。
→底辺のＢＲとＡＱの長さは等しい。

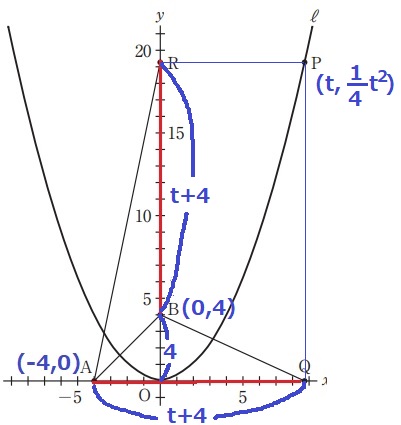
Ｐのｘ座標をｔとする。Ｐ（ｔ、１/４ｘ²）
ＡＱ＝ＢＲ＝ｔ＋４
Ｐのｙ座標で等式を立てる。
１/４ｔ²＝ｔ＋８
ｔ²＝４ｔ＋32
ｔ²－４ｔ－32
＝（ｔ－８）（ｔ＋４）＝０
ｔ＞４より、ｔ＝８
Ｐのｘ座標は８。

大問４（平面図形）

（１）

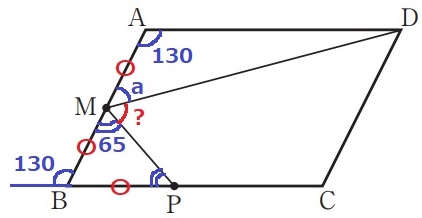
ＡＤ//ＢＣの錯角で130°を下におろす。
二等辺三角形ＢＭＰで外角定理→∠ＢＭＰ＝130÷２＝65°
∠ＤＭＰ＝180－65－ａ＝（115－ａ）°
エ

（２）
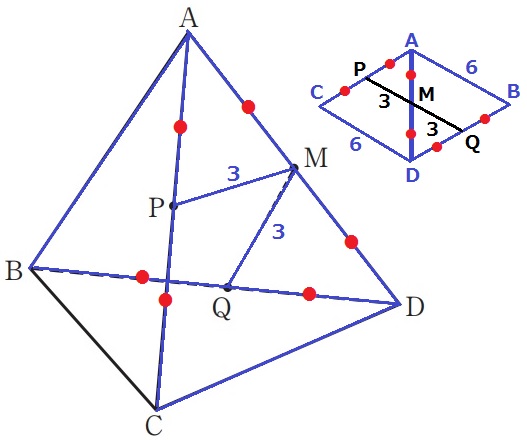
△ＡＭＤ∽△ＣＱＰの証明。

平行四辺形の対角は等しい。∠ＭＡＤ＝∠ＱＣＰ
ＡＢ//ＤＣの錯角、ＤＭ//ＱＰの同位角で∠ＡＭＤ＝∠ＣＱＰ
２角が等しく∽。

②
ＰＱは△ＣＰＱの１辺。ＭＲは△ＡＭＤの１辺の一部。
そこで前問の△ＡＭＤ∽△ＣＱＰが使えないか模索する。

ＢＰ：ＰＣ＝②：①
対辺ＡＤ＝③
△ＡＭＤ∽△ＣＱＰより、ＡＭ：ＣＱ＝③：①、ＤＭ：ＰＱ＝③：①

ＭはＡＢの中点なので、ＭＢ＝③
ＤＱ＝⑥－①＝⑤
△ＡＭＲ∽△ＱＤＲより、ＭＲ：ＲＤ＝３：５
ＭＲ＝③×３/８＝〇９/８
ＰＱ：ＭＲ＝①：〇９/８＝８：９
う…８、え…９

大問５（空間図形）

（１）

Ｐ・Ｍ・Ｑは各辺の中点。
△ＡＰＭと△ＡＣＤ、△ＤＭＱと△ＤＡＢに中点連結定理を適用。
ＭＰ＝ＭＱ＝６÷２＝３ｃｍ

ＰＱに補助線。△ＡＣＱをとらえる。
ＡＱは正三角形ＡＢＤの高さ。１：２：√３の直角三角形からＡＱ＝３√３ｃｍ
同様に、ＣＱは正三角形ＢＣＤの高さ。ＣＱ＝３√３

△ＡＣＱは等辺が３√３の二等辺三角形。
頂角Ｑから底辺ＡＣの中点であるＰを結ぶと、ＱＰ⊥ＡＣとなる。
△ＡＰＱで三平方→ＰＱ＝３√２ｃｍ

△ＭＰＱの各辺の比は。３：３：３√２＝１：１：√２
△ＭＰＱは直角二等辺二等辺で、∠ＰＭＱはこの頂角だから90°
お…９、か…０

＠別解＠

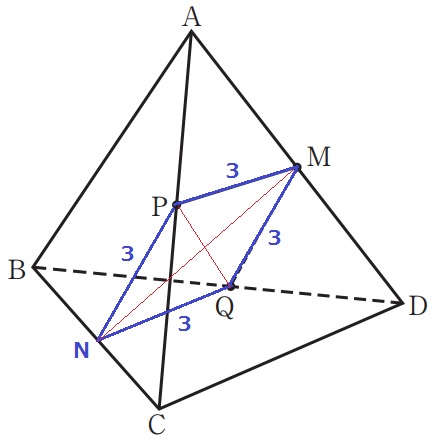
ＢＣの中点をＮとする。
中点連結定理でＰＮ＝ＮＱ＝３ｃｍ
四角形ＰＮＱＭは４辺が等しい菱形である。
ここから対角線ＰＱ＝ＭＮがいえないか。。

ＭＮは△ＢＣＭの高さ、ＱＰは△ＡＣＱの高さである。
ＢＣ＝ＡＣ＝６ｃｍ
ＭＢとＭＣ、ＱＡとＱＣは側面の正三角形の高さにあたり、すべて長さが等しい。
３辺が等しく、△ＢＣＭ≡△ＡＣＱとなり、これらの高さにあたるＭＮ＝ＱＰがいえる。
菱形ＰＮＱＭの２本の対角線が等しいことから、四角形ＰＮＱＭは正方形である。
∠ＰＭＱ＝90°

（２）

三角錐Ｍ－ＢＣＤの底面を△ＢＣＤ、三角錐Ｍ－ＡＰＱの底面を△ＡＰＱとすると、
ＭＤとＭＡが同一直線上にあるので、高さの比はＭＤ：ＭＡとなる。
ＡＭ＝ＭＤだから、高さが等しい！
ということは、三角錐Ｍ－ＢＣＤと三角錘Ｍ－ＡＰＱの体積比は、
底面積である△ＢＣＤ：△ＡＰＱの面積比に相当する。

８秒後のＰはＣから４ｃｍ、ＱはＢから４ｃｍのところにあり、
ＣＰ：ＰＢ＝ＢＱ：ＱＡ＝４：８＝１：２

△ＢＣＤの面積を１とする。
【△ＡＢＣ⇒△ＡＢＰ⇒△ＡＰＱ】
１×２/３×２/３＝４/９
立体Ｍ－ＢＣＤ：立体Ｍ－ＡＰＱ＝１：４/９＝９：４
したがって、立体Ｍ－ＢＣＤは立体Ｍ－ＡＰＱの９/４倍。
き…９、く…４

＠2021年度・都立解説＠
数学…平均53.3点　社会…平均54.6点　理科…平均47.8点　英語…平均54.1点
公立高校入試解説ページに戻る