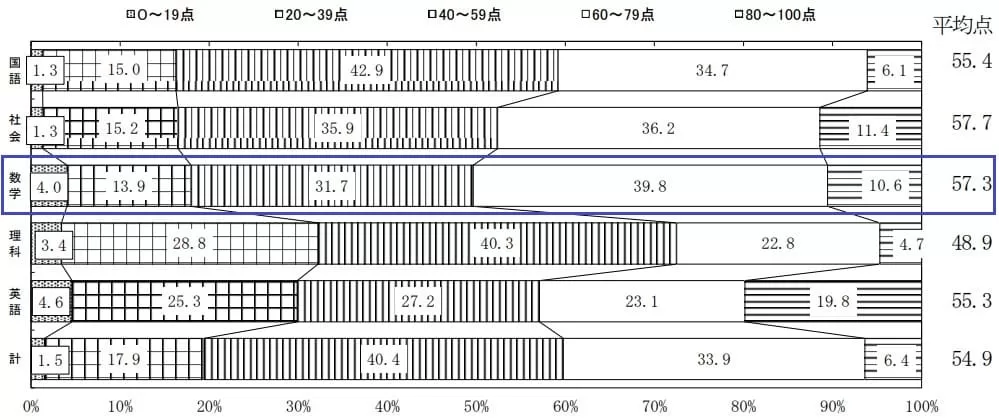
平均57.3点（前年比；＋5.5点）
問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１） 96.8％
－３－（－９）
＝－３＋９
＝６
（２） 95.7％
20ｘｙ2÷（－４ｘｙ）
＝－５ｙ
（３） 96.2％
４√３－√12
＝４√３－２√３
＝２√３
（４） 90.5％
ｘ2＋２ｘ－８
＝（ｘ－２）（ｘ＋４）
（５） 74.1％
反比例の比例定数ａはｘとｙの積で一定。
ａ＝－６×２＝－12（ｙ＝－12/ｘ）
ｘ＝－12÷３＝－４
（６） 43.8％
円錐の側面積…母線×半径×π
６×３×π＝18πｃｍ2
（７） 88.6％
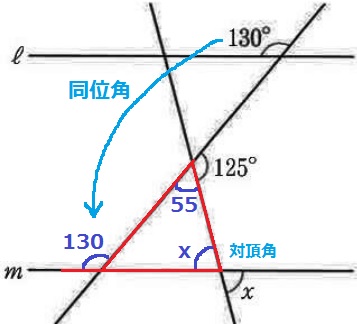
対頂角でｘ、同位角で130°を移動。
180－125＝55°
赤線の三角形で外角定理で、ｘ＝130－55＝75°
（８） 84.5％
抽出した50個において、糖度10～14は15個。
母集団1000個においても50個中15個の割合だと推定する。
1000×15/50＝300個
ウ
＠備考＠
兵庫県はイチジク生産量が多いらしい。
大問２（数量変化）
（１） 70.2％
１秒後にＰとＱはそれぞれＯＡ、ＯＢの中点にある。
中点連結定理で、ＰＱ＝４÷２＝２ｃｍ
（２） 31.2％！
２秒後にＰはＡ、ＱはＢに着き、△ＯＰＱの面積は最大になる。
底辺ＯＰと高さＰＱがともに伸びるので、面積はｙ＝ａｘ2の形で増加する。
ア
（３）① 76.7％
２秒後の△ＯＰＱの面積は△ＯＡＢに同じ。
２×４÷２＝４
② 55.1％
ＡＢ＝４ｃｍ
図２より、ＰはＡに着いてから８秒後にＢに着く。
Ｐの速さは、４÷８＝秒速１/２ｃｍ
③ 8.9％!!
２秒後に△ＯＰＱの面積は増加から減少に転じる。
面積が等しくなったということは、ｔは２秒前、ｔ＋４は２秒後。
図２のグラフを活用する。
０≦ｘ≦２：ｙ＝ａｘ2に（２、４）を代入してｙ＝ｘ2
２≦ｘ≦10：傾きは前問で求めたＰの速さから－１/２。
（２、４）から左に２、上に１移動して、切片は４＋１＝５→ｙ＝１/２ｘ＋５
ｙ＝ｘ2とｙ＝－１/２ｘ＋５に、それぞれｔとｔ＋４を代入したｙの値が等しくなる。
ｔ2＝－１/２（ｔ＋４）＋５
ｔ2＋１/２ｔ－３＝０ ←２倍
２ｔ2＋ｔ－６
＝（２ｔ－３）（ｔ＋２）＝０
ｔ＞０より、ｔ＝３/２
大問３（平面図形）
（１）ⅰ…83.2％、ⅱ…91.8％
∠ＡＣＤ＝∠ＣＡＤの証明。
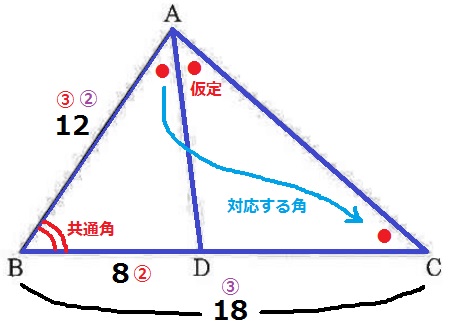
最初に△ＡＢＣ∽△ＤＢＡを証明する。
ＡＢ：ＤＢ＝12：８＝③：②
ＣＢ：ＡＢ＝18：12＝③：②
共通角と合わせ、２辺とあいだの角が等しいから△ＡＢＣ∽△ＤＢＡ
対応する角から、∠ＡＣＢ＝∠ＤＡＢ
仮定から∠ＤＡＢ＝∠ＤＡＣなので、∠ＡＣＤ＝∠ＣＡＤがいえる。
ⅰ…ア、ⅱ…オ
（２） 68.6％
ＤＣ＝18－８＝10ｃｍ
前問より、△ＡＤＣは底角が等しいから二等辺三角形。
ＡＤ＝10ｃｍ
（３） 51.4％
前問の活用。
△ＡＢＣ∽△ＤＢＡの相似比は、ＡＢ：ＤＢ＝３：２
ＡＣ＝10×３/２＝15ｃｍ
＠別解＠
公立高校入試で角の二等分線の定理…ヽ(`Д´)ﾉﾒｯ!
という方もいるようなのですが、サボは別に良いと思います。
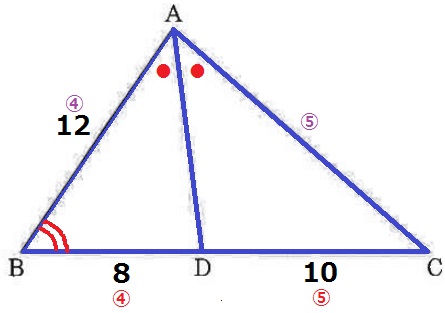
角の二等分線の定理からＡＢ：ＡＣ＝ＢＤ：ＣＤ＝④：⑤
ＡＣ＝12×⑤/④＝15ｃｍ
（４） 0.5％!!!
図形の特徴を少しずつ紐解いていく。
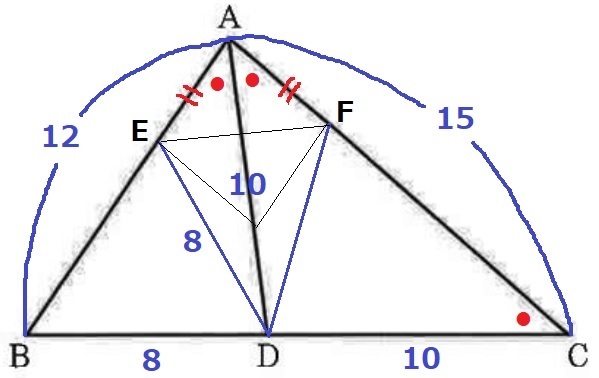
ＥとＦを記す。菱形は４辺が等しい→ＡＥ＝ＡＦ
求めたいのはＡＥ、ＡＦを１辺とする菱形の面積比だが、
ＥＦが菱形の対角線なので△ＡＥＦの面積比を２倍すればいい。
ＡＥとＡＦの長さが知りたい。
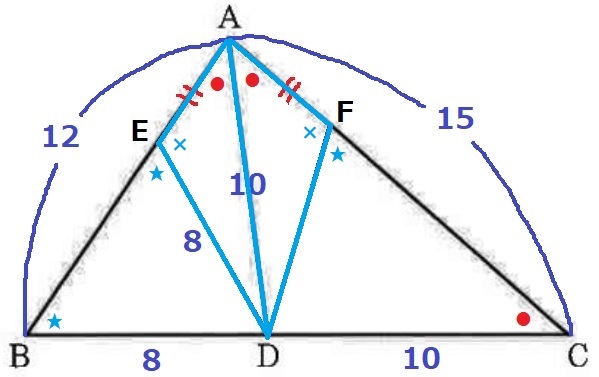
△ＡＥＤと△ＡＦＤに注目すると、
ＡＥ＝ＡＦ、共通辺ＡＤ、仮定の∠ＤＡＥ＝∠ＤＡＦから、
２辺とあいだの角が等しく合同。
対応する角で、∠ＡＥＤ＝∠ＡＦＤ（×）
二等辺三角形ＤＥＢの底角を★とする。
★＋×＝180°なので、∠ＤＦＣ＝180－×＝★
今度は△ＡＢＤと△ＣＦＤに着目する。
２角の★と●が等しい→残りの角で∠ＡＤＢ＝∠ＣＤＦ
１辺と両端角が等しく、ここにも合同図形が隠れていた。
ＦＣ＝ＢＡ＝12ｃｍ
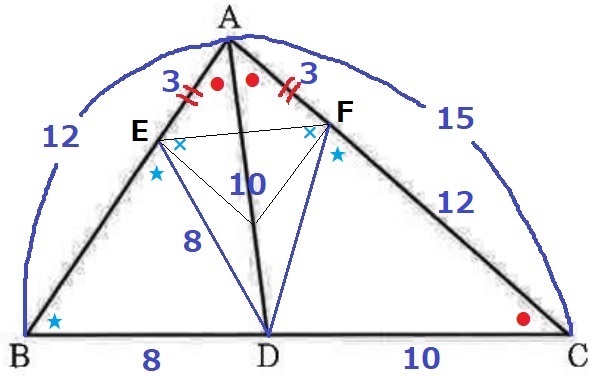
ＡＦ＝ＡＥ＝15－12＝３ｃｍ
隣辺比で△ＡＥＦの面積比を算出し、それを２倍すれば菱形になる。
１×３/12×３/15×２＝１/10倍
＠別解＠
菱形の対角線は垂直に２等分するので、ＡＤを対称の軸とするとＥとＦは対称関係にあります。
ＡＤが∠ＢＡＣの二等分線であることから、Ｂを反対側に持ってくるとＡＣ上にきます。
△ＡＢＤを対称移動させて△ＡＢ’Ｄとすると、ＡＢ’＝12ｃｍ、ＤＢ’＝８ｃｍ
Ｂ’Ｃ＝15－12＝３ｃｍ
今度は、二等辺三角形ＤＣＡの中に二等辺三角形ＤＢ’Ｆがある点に注目すると、
対称の軸である底辺の垂直二等分線が共有され、対称性からＡＦ＝ＣＢ’＝３ｃｍと求まります。
大問４（関数）
（１） 84.9％
Ａはｙ軸についてＢと対称。
Ｂのｘ座標が２だから、Ａのｘ座標は－２。
（２） 83.8％
ｙ＝ａｘ2に（２、－１）を代入。
－１＝４ａ
ａ＝－１/４
（３） 51.7％
Ａ（－２、４）→Ｃ（２、－１）
右に４、下に５だから、傾きは－５/４。
ｙ＝－５/４ｘ＋１に（ｘ、ｙ）＝（２、－１）を代入。
－１＝－５/４×２＋ｂ
ｂ＝３/２
ｙ＝－５/４ｘ＋３/２
（４）① 32.1％！
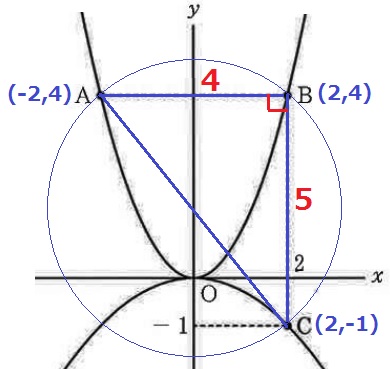
直径に対する円周角は90°→円の直径はＡＣ。
ＡＢ＝２－（－２）＝４ｃｍ
ＢＣ＝４－（－１）＝５ｃｍ
△ＡＢＣで三平方→直径ＡＣ＝√41ｃｍ
② 7.0％!!
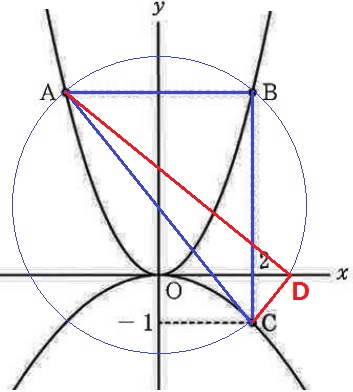
↑円Ｏ’とｘ軸が交わる、ｘ座標が正の点Ｄはココ。
直径ＡＣの中点がＯ’の中心である。
ＡとＣのｘ座標から中心はｙ軸上にある→ＡＣの切片が円Ｏ’の中心。
切片をＥとする。（３）からＥＯ＝３/２ｃｍ
半径ＥＤ＝√41/２ｃｍ
△ＥＯＤで三平方→ＯＤ＝２√２ｃｍ
ｘ＝２√２
大問５（確率）
（１） 88.1％
６の約数は１・２・３・６。
箱に入れる玉は４個。
（２） 25.6％！
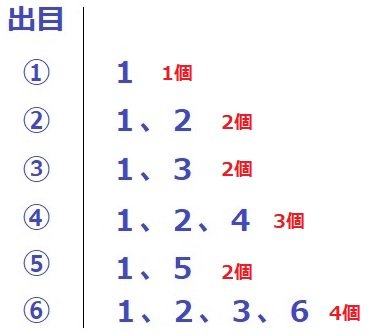
各出目で入れる玉の個数を確認しておく。
１回の操作で必ず１個は玉を入れる。
２回の操作で合計４個となるには、２＋２か１＋３のどちらか。
●２個＋２個
②、③、⑤のどれかを連続して出せばいい。
３×３＝９通り
●１個＋３個
（①、④）か（④、①）の２通り。
計11通り。
全体は６×６＝36通りだから、確率は11/36。
（３）① 37.8％
どの出目がでても１の玉は１個いれる。
→操作ごとに１の玉は１個ずつ増えていく。
１の玉が21個ということは、操作は21回行われた。
ｎ＝21
② 19.1％！
出目①が２回；玉は２個。
出目⑤が５回；玉は10個。
これらを除外すると、残り回数は21－７＝14回
残りの玉は52－12＝40個
出目③と⑤は回数は同じ。
『４の玉と６の玉が同じ数』→４の玉は４、６の玉は６のときに１個ずつ入れる。
→出目④と⑥の回数も同じ。
③＋⑤をセットで考えると、玉は２＋２＝４個、
同様に、④＋⑥のセットでは玉は３＋４＝７個入れる。
２つにまとめるので、セットの回数は14÷２＝７回
③＋⑤のセットをｘ回とすると、④＋⑥のセットは７－ｘ回。
４ｘ＋７（７－ｘ）＝40
ｘ＝３
③と⑤は３回ずつ出た→３回。
＠別解＠
もしくは、４ａ＋７ｂ＝40と不定方程式にして、
４ａと40が４の倍数だから、７ｂも４の倍数。
40以下では４×７＝28しかないのでｂ＝４、ａ＝３
③ 5.5％!!
出目④と⑥は、７－ｘ＝７－３＝４回ずつ出した。
出目⑤は３回→５の玉は３個。
残りの玉は、52－３＝49個
６の約数ではない玉は４か５なので、４の玉を除外すればいい。
４の玉は出目④のみで、４回出したから４個。
49－４＝45個
６の約数（１、２、３、６）を取り出す確率は45/49。
大問６（文字式）
（１） 82.1％
作業通りに枚数を調べる。
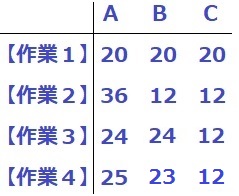
箱Ａは25枚。
（２）ⅰ…80.9％、ⅱ…67.7％、ⅲ…71.6％
上図のとおり、【作業３】後のＡは24枚。
最初のコインをｘ枚ずつとして作業の流れを確認する。
【作業２】後のＡはＢとＣからそれぞれ８枚ずつ足され、ｘ＋16枚。
Ｃはｘ－８枚。【作業３】でＡは、（ｘ＋16）－（ｘ－８）＝24枚となる。
ⅰ…24、ⅱ…ｘ＋16、ⅲ…ｘ－８
（３）① 34.0％
【作業２】でＢとＣから取り出すコインをａ枚とする。
Ａの枚数はｘ＋２ａ枚、Ｃの枚数はｘ－ａ枚。
【作業３】後のＡは、（ｘ＋２ａ）－（ｘ－ａ）＝３ａ
ａは自然数だから、３ａは３の倍数。
ｎ＝３
② 16.3％！
【作業４】後のＡは３ａ＋１枚。
選択肢の中で、３の倍数＋１は55（ウ）。
３ａ＋１＝55
ａ＝18
ＢとＣから１枚のコインを取り出せばいい。
ウ、18枚
完走するのは時間的にシビアかもしれない。前半の基本的な小問で得点を積み重ねる。
大問１
（６）側面積なのに表面積を求める人が一定数いる。
（８）標本調査が絡む度数分布表。２つの階級を合計する。
大問２
最後以外は確実にとっておきたい。
（３）③Ｐが途中で変速するが、グラフの問題に落とし込めば式が立てられる。
図２は一次関数しかないので、２秒前の放物線を記す。
２秒後に増⇒減だから、ｔがｙ＝ａｘ2、ｔ＋４が一次関数上にある。
大問３
（３）までは取る。対応する辺が見えづらかったら、図形を描いてみる。
（４）おそらく最も正答率が低い。
菱形をもってきたのは、おそらく対称性の利用かと思われる。
菱形のもう１つの頂点はＡＤ上にあり、ＥとＦが対応する点とわかれば、
△ＡＥＤ≡△ＡＦＤが見えやすくなる。
２つの二等辺三角形と３つの不等辺三角形からなる興味深い構図であった。
大問４
（４）②Ｄのおよその位置を見極める。
半径を斜辺とする直角三角形で三平方の定理を使う。
大問５
情報整理に時間をとられる。
各出目でどの玉を入れるかを素早く出しておく。
（３）①地味に思考力が問われる。
②方程式の問題だと方針は見えやすいが、立式の複雑さに焦って蒸発しそう。
同数同士は固めて（③⑤）（④⑥）にまとめると、少しやりやすくなる。
③②ができれば、③は比較的早く解答できる。
大問６
丁寧に条件文を読んでいけば解けるが、どれだけ時間を残せたかによる。
（２）Ａの流れと【作業２】後のＣを調べれば足りる。
（３）適当な文字を置いて式を立てる。①ができれば②も正解しやすい。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント
スミマセン。2023年兵庫県公立高校入試理科の解説はありますでしょうか？
コメントありがとうございます。
いろいろな問題の解説を書きたい気持ちはあるのですが、一人だとなかなか厳しいものです。
現在、高校入試の解説は千葉・東京・神奈川の３つに絞っております。
何卒、ご了承くださいませ。
サボ
こんにちは!!
中学3年生のみくです。
今回の入試の解説を見たときすごくわかりやすかったです!!
過去問の本には解説が詳しく乗っておらずインターネットで調べたときにこの「家庭教師サボの部屋」というサイト
を見つけ最初は文字がたくさんですごく読むのが大変だったけど、この解説を見てとても分かりやすかったです。
これからもこのサイトを見ながら分からないところを解決して行きます!!
みくさんへ
コメントありがとうございます(´ω`)
そう言ってくださると、とても励みになります。
私の解説は長くなりがちなので、カットしながら読んでくださいませ。
兵庫は書いていませんが、目次から様々な科目を書いていますのでご覧ください。
社会は長いので直前期に読む代物ではありませんが。。
何か質問があったら気兼ねなくどうぞです。受験、応援しています(*´ω`*)
サボ