2019年度　滋賀県公立高校入試問題過去問【数学】解説

平均38.1点

問題はコチラ→リセマムさん

大問１（小問集合）

（１）　84.5％
１５－１９＝－４

（２）　73.5％
１/４ａ－５/６ａ＋ａ
＝５/１２ａ

（３）　80.8％
連立方程式。代入法でもやりやすいかな？
ｘ＝３、ｙ＝－２

（４）　78.8％
√２７＋１２/√３
＝３√３＋４√３
＝７√３

（５）　71.4％
２ｘ²＋４ｘ－７＝ｘ²－２
ｘ²＋４ｘ－５
＝（ｘ－１）（ｘ＋５）＝０
ｘ＝－５、１

（６）　61.4％
１４ｘ²ｙ÷（－７ｙ）²×２８ｘｙ
＝１４ｘ²ｙ÷４９ｙ²×２８ｘｙ
＝８ｘ³

（７）　24.5％！
－２８＝－７ｘ²
ｘ²＝４
ｘ＝±２
*ｙ＝ａｘ²なので、ｙ座標が同一のｘ座標は２つある！

（８）　33.0％！
ａ：青玉が出る確率は３/６＝１/２
２回連続で出すので、１/２×１/２＝１/４

ｂ：青と白を出す。
青は１/２、白は１/３。（青白）（白青）の２通り。
１/２×１/３×２＝１/３

ｃ：ａとｂを比較。
ｂの方が確率が高いのでイ。

（９）①　55.0％
△ＡＢＣ∽△ＤＢＥ（２角相等）
ＡＢ：ＢＣ＝ＤＢ：ＢＥ
９：６＝ＤＢ：３
ＢＤ＝９×３÷６＝９/２

②　3.8％!!
旧千葉の作図を彷彿させる。
二等辺三角形の底辺と平行な線分を引き、面積を半分にする。

ＡＦ：ＡＢ＝１：√２にすればいい。
√２といえば…直角二等辺三角形の斜辺。

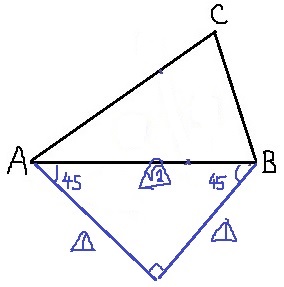
ＡＢを斜辺とする直角二等辺を作図。

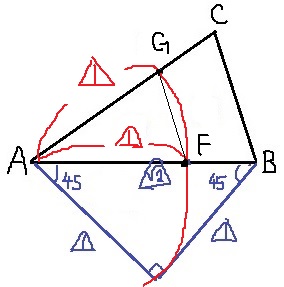
△１を移動すれば、Ｆ・Ｇがでてくる。
ＦとＧはＡから等距離にあるので、自ずとＦＧ//ＢＣとなる。

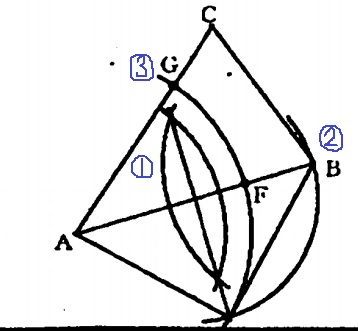
↑公式解答より。
①ＡＢの垂直二等分線
②ＡＢの中点を基準にＢ→①の線。交点が直角二等辺の頂角。
③Ａから頂角の長さをとって、ＡＢ、ＡＣに移動。交点がＦとＧ。

大問２（データの活用）

（１）　81.6％
標本の選び方。
母集団が全校生徒なので、全校生徒からランダムに選ぶ→エ

（２）　53.1％
50個より多く持ってきた人は、30人のうち12人。
これは母集団でもわからないものとする。
４８５×１２/３０＝１９４人

（３）解答例：階級の幅を小さく設定した図２の方が、各階級の度数を詳しく調べることができ、
平均値が含まれる階級に最頻値がないことがわかる。　8.5％!!
*図２の方が分布の特徴がよくわかる理由を、指定語句を使って述べる。
図１では平均値が含まれる階級の度数が最も多いが、
図２ではそうではない点は指摘しておきたい。
階級の幅を小さくするとバラツキの度合いを詳しく見られる。

（４）①　49.0％
ヒストグラムを使った推論問題。
平均値を５回出すのはさすがにしんどいので、中央値だけ求めてみよう。
３０人の中央値は15と16の平均値。
【Ⅰ…７０　Ⅱ…５０　Ⅲ…７０　Ⅳ…５０　Ⅴ…５０】
Ｂ・Ｃ・Ｄの中央値は同じなので、Ａ・ＥがⅠかⅢ。
Ｅの中央値は最頻値と平均値が同じ階級にあるとのことなので、
Ⅰはバラツキがあるから、山なりのⅢがＥ組となる。
よって、Ｅ組の最頻値が含まれる階級は６０以上８０未満。

②　25.4％！
前問より、ⅠがＡ組となる。
Ａ組とＤ組の平均値は同じなので、Ａ組の平均値を求めればいい。
階級値は階級の平均で計算。
１０×６＋３０×６＋５０×２＋７０×５＋９０×８＋１１０×３＝1740
1740÷３０＝５８

Ｂ・Ｃ・Ｄ組のヒストグラムがわからなくても出せてしまう。
一応、検討すると、Ｂ組はＣ組より範囲（レンジ）が小さい。
Ⅱ・Ⅳ・Ⅴのうち、唯一範囲が20-100であるⅤがＢ。
Ⅱ・Ⅳで60個以上の人が多いⅡがＤ。残りのⅣがＣ。

大問３（等式の変形）

（１）　15.8％！
コップのふちは直径９ｃｍの円。
この11周分が円Ｏの円周に匹敵する。
９π×１１＝２πｒ
２ｒ＝９９
ｒ＝９９/２＝４９．５ｃｍ

（２）
コップを９回転させてグルっと１周するので、
１回転では円周の９分の１を周る。
３６０×１/９＝４０°　29.3％！

コップの回転数ｍが増える→コップを多く回転させなければ１周しない。
１回転あたりの移動距離（弧ＳＡ）は短くなるので、中心角ｙの値は小さくなる。
ｙ＝360/ｍの反比例式を挙げて、ｍが大きくなるとｙが小さくなる点を指摘する。
記号：イ　15.3％！

（３）　0.2％!!!
半径ＡＯをｘで表して算出。

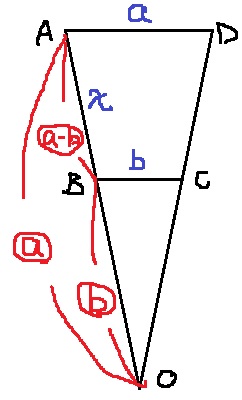
△ＡＯＤ∽△ＢＯＣから、ｘは○ａ－ｂ。
ＡＯ（○ａ）をｘで表すと、
ｘ×ａ/（ａ－ｂ）＝ａ/（ａ－ｂ）・ｘ

ａπ×ｍ＝ａ/（ａ－ｂ）・ｘ×２π　←両辺からπ削除
ａｍ＝２ａ/（ａ－ｂ）・ｘ　←両辺を×（ａ－ｂ）/２ａ倍、左辺のａを約分
ｘ＝ｍ（ａ－ｂ）/２

公式解答では、ＡＢ（ｘ）＝ＡＯ－ＢＯであることから、
ＡＯ…ＡＯを半径とする円周＝コップのふち×回転数ｍ
ＢＯ…ＢＯを半径とする円周＝コップのふち×回転数ｍ
最後にＡＯ－ＢＯで算出している。

ちなみに、円錐を転がしたときの円錐の回転数は〔母線÷半径〕で求められます。

大問４（平面図形）

（１）　23.3％！

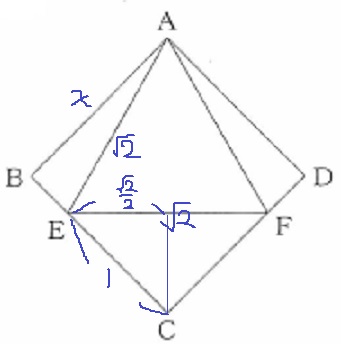
△ＡＢＥで三平方。
ＢＥ＝√（２－ｘ²）

もしくは、△ＥＣＦが直角二等辺三角形なので、
斜辺ＥＦ＝√２から、ＥＣ＝１
ＢＥ＝ｘ－１となる。

（２）①　1.1％!!
ＰがＢＦの中点であることを証明する。
合同や相似以外の証明に慣れていないと書き方に迷う。

ＢＥに補助線。ＡＢもＥＦも正六角形の１辺なので同じ長さ。
Ｓ・Ｕは各々の中点なので、ＡＳ：ＳＢ＝ＦＵ：ＵＥ
平行線と線分の比から、ＡＦ//ＳＵ//ＢＥ
△ＡＢＦに注目。すると、中点連結定理に出てくる形があり、
ＢＰ：ＰＦ＝ＢＳ：ＳＡ＝１：１→ＰはＢＦの中点となる。

②　6.5％!!
正六角形全体の面積は４０√３。
６つに分割すると正三角形になる。

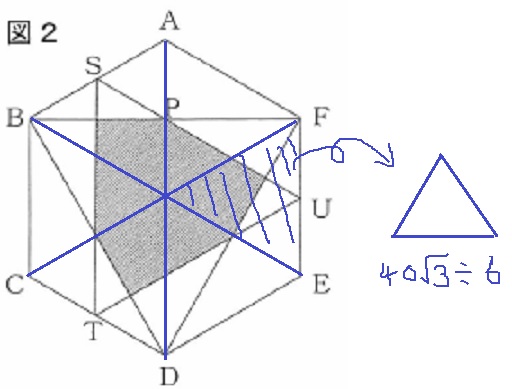
この正三角形の１辺を求めればいい。
１辺をｘとする。高さは√３/２・ｘ。
ｘ×√３/２・ｘ×１/２＝４０√３÷６
ｘ²＝８０/３
ｘ＝４√１５/３

③　0.7％!!!
中にある２つの正三角形の他の交点も中点にある。

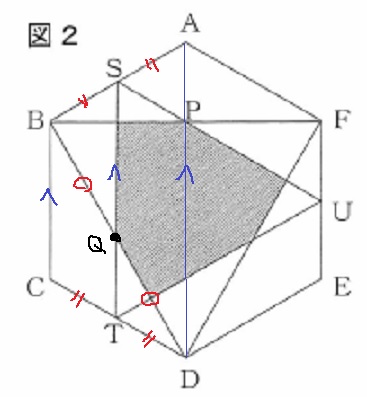
ＢＤとＳＴの交点をＱとする。
①と同じように考えると、ＱはＢＤの中点にある。

同様に、ＤＦとＴＵの交点ＲもＤＦの中点にある。

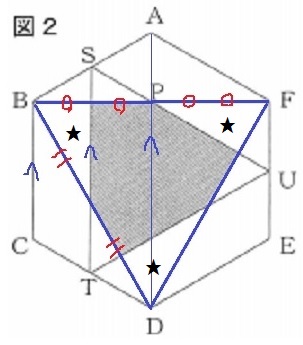
辺ＢＦにおいて、ＳＴとの交点はＢＦの４分の１。
正三角形ＢＤＦから★３つ分をひけば、斜線部の面積が出てくる。

△ＢＤＦは正六角形の半分。
左上の★の部分は、△ＢＤＦ＝⑧とおくと①に相当する。

４０√３×１/２×５/８＝２５√３/２

＠余談＠

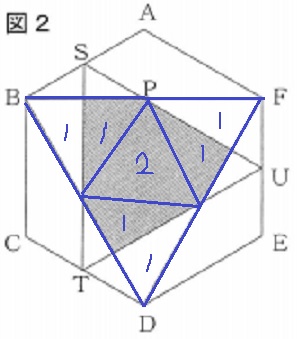
この形が見えたら一発ね！ 

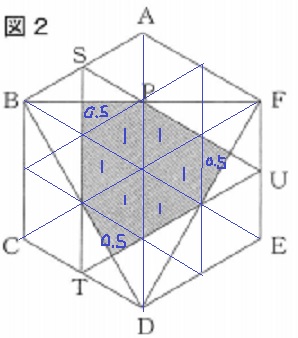
全体を㉔とおくと斜線部分は〇7.5
４０√３×7.5/２４＝２５√３/２

＠追記＠
芝中学で同じ形がでてました。
正六角形の分割方法はいくつか覚えておいた方がいいかもしれません。
公立高校入試解説ページに戻る