2019年度　鳥取県公立高校入試問題過去問【数学】解説

平均27.3点（50点満点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）①　97.0％
－7＋3－４
＝－８

②　95.9％
１/３÷（－１/６）
＝１/３×（－６）
＝－２

③　85.8％
３/√３＋４√３－√27
＝√３＋４√３－３√３
＝２√３

④　91.4％
４（２ｘ－１）－３（２ｘ－３）
＝８ｘ－４－６ｘ＋９
＝２ｘ＋５

⑤　75.1％
（－ｘｙ）²×10ｘｙ²÷５ｘ²
＝ｘ²ｙ²×10ｘｙ²÷５ｘ²
＝２ｘｙ⁴

（２）　75.6％
（３ｘ－１）（４ｘ＋３）
＝12ｘ²＋９ｘ－４ｘ－３
＝12ｘ²＋5ｘ－３

（３）　82.7％
ａ²－２ａ
＝（－３）²－２×（－３）
＝９＋６＝15
*ａ（ａ－２）＝－３×（－３－２）＝15でも可。

（４）　87.3％
ｘ²－４ｘ＋３
＝（ｘ－１）（ｘ－３）

（５）　77.7％
Ｖ＝πｒ²ｈ　←両辺を÷πｒ²して左右をひっくり返す。
ｈ＝Ｖ/πｒ²

（６）　91.4％
円周角定理から、∠ＢＯＣ＝70×２＝140°
半径より、ＯＢ＝ＯＣ→△ＯＢＣは二等辺。
∠ｘ＝（180－140）÷２＝20°

（７）　78.2％
５ｘ²＋３－１＝０
因数分解ができないので解の公式を適用。
ｘ＝（－３±√29）/10

（８）　31.5％！（部分点25.9％、無答16.8％）
整数の証明。
（２ｎ＋１）²＋19
＝４ｎ²＋４ｎ＋１＋19
＝４ｎ²＋４ｎ＋20
＝４（ｎ²＋ｎ＋５）
ｎは整数なので、ｎ²＋ｎ＋５も整数だから、
４（ｎ²＋ｎ＋５）は４の倍数となる。

（９）　51.8％（部分点7.6％、無答15.7％）
合同の証明。レベルは易。
仮定よりＡＭ＝ＣＭ
この両端角が錯角（ＡＤ//ＢＣ）と対頂角で等しくなる。
一辺両端角相等から合同。

（10）　14.7％！（部分点14.7％、無答26.9％）
√２の作成。
１と√２といえば…直角二等辺三角形。

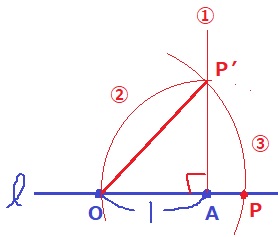
①Ａを通る、ℓに垂直な垂線を作図。
②Ａを中心に４分の１円を描く。交点をＰ’とする。
③Ｏを中心にＰ’をℓ上に移動。交点がＰ。

大問２（データの活用）

（１）　79.7％
最頻値（モード）は最も表れている値。
30～40点が多い。
必ず階級値で答える→35点

（２）　37.1％（部分点36.5％）
階級の幅を10から５にチェンジすると、より詳細な分布状況が得られる。
ア：最頻値が57.5点に変わっている。×
イ：40点以上と40点未満の人数の結果は変わらない。×
ウ：最小値も最大値も変化しないので、範囲（レンジ）も変わらない。〇
あくまで分布が詳しく見られるのであって、それそれの点数は変化しない。
エ：点数は変化しないので、平均は変わらない。
50人の中央値（メジアン）は25番目と26番目の平均で、これも変わらない。〇
ウ・エ

大問３（確率）

（１）　73.1％
確率なので、「必ず」「常に」といった断定はできない。
大数（たいすう）の法則から試行回数を増やすと、４分の１に近づいていく。
ア

（２）　72.1％
そうたは４枚から４を出す→１/４
よしこは残りの３枚から２を出す→１/３
１/４×１/３＝１/12

（３）　48.2％（部分点3.0％、無答11.2％）
解答では理由の記述が求められる。
奇数の確率と偶数の確率を計算して比べればＯＫ。
◆奇数（そうたの勝利）
（１、２）（１、４）（２、３）（３、４）
および、これらの逆から８通り。
全体が４×３＝12通りなので、８/12＝２/３

◆偶数（よしこの勝利）
和が偶数は、全体から奇数をひけばいい。
12－８＝４通り
４/12＝１/３

そうたの勝率は２/３で、よしこの勝率は１/３だから、
そうたの方が勝ちやすくなる。
*和が偶数となるのは、奇数同士か偶数同士しかないのでパターンが少ない。

大問４（文字式）

（１）①　81.2％
200人の43％を求める。
200×43/100＝86人

②　76.1％
１回目と２回目で、参加人数は200人で変わらない。
中級は８％増加したので、200×８/100＝16人

（２）①ア：80.7％、イ：54.8％、ウ：28.4％！
誘導に従い、穴埋めしていく。
文章を丁寧に読み込むこと！空欄に書くべき内容を外さないように。
全参加人数はＡ～Ｃ中学校の参加人数の和。
ア…ｘ＋ｙ＋200

２回目の上級のみ見る。
Ａ校の43％は前問でだした86人。
Ｂ校はｘの40％、Ｃ校はｙの25％。
これらを合算すると、２回目上級コースの３校合計人数となる。
イ…40/100ｘ＋25/100ｙ＋86

iiなので、今度は１回目と２回目の中級コースを比較する。
Ａ校は８％増加し、これは前問でだした16人。
Ｂ校は５％増、Ｃ校は15％増。
３校で60人増加したので、増加分で等式を作成する。
ウ…５/100ｘ＋15/100ｙ＋16（＝60）

②　8.6％!!（無答60.4％）
前問の正解が前提条件。
40/100ｘ＋25/100ｙ＋86＝35/100（ｘ＋ｙ＋200）…①
５/100ｘ＋15/100ｙ＋16＝60…②
うえの連立を解く。計算ミスに注意！
５ｘ－10ｙ＝－1600…①’
５ｘ＋15ｙ＝4400…②’
ｘ＝160、ｙ＝240

大問５（数量変化）

（１）　84.8％
ｙ＝ａｘにＡ（２、８）を放り込む。
８＝２ａ
ａ＝４

（２）　61.9％
ｘ＝２のとき、ｙ＝８
ｘ＝８のとき、ｙ＝２
２≦ｙ≦８

（３）①　22.8％！（部分点1.5％、無答35.0％）
問題文のおさらい。

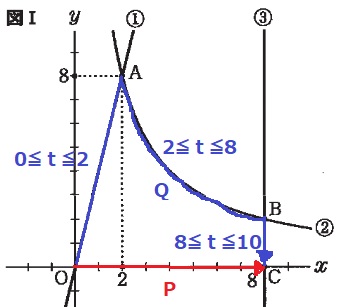
Ｐはｘ軸上を毎秒１ｃｍで進む。８秒後でＣに止まり、動かない。
Ｑは①→②→③と動き、常にＰの真上にくる。
８≦ｔ≦10では、③上をＣに向かい、10秒後にＰとＱが出会う。

０＜ｔ≦２のとき、△ＯＰＱは底辺と高さがともに増えていくので、
その面積はｙ＝ａｘ²で増加する。
Ａ（２、８）を代入。
８＝２²ａ
ａ＝２
ｙ＝２ｘ²

ｘは時間ｔ、ｙは△ＯＰＱの面積Ｓなので文字を置き換えること！
Ｓ＝２ｔ²

②　10.2％！（部分点26.9％、無答35.5％）
先に解答から。

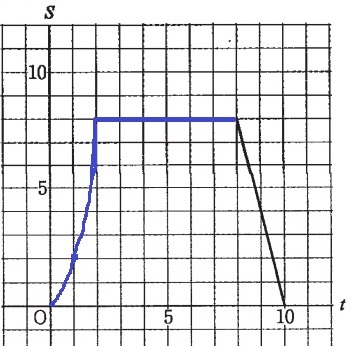
０≦ｔ≦２は、前問のＳ＝２ｔ²
（１、２）を通過するように書こう。

問題は、Ｑが②上にあるとき（２≦ｔ≦８）。
反比例はｘ座標とｙ座標の積が比例定数で一定。
②：ｙ＝16/ｘ
ｘｙ＝16
ｘとｙの積が常に16だから、Ｓ＝ｘｙ÷２＝８で一定。
２≦ｔ≦８は横線になる。

③　6.1％!!（部分点11.2％、無答51.3％）
先ほどのグラフにＳ＝５を追加。

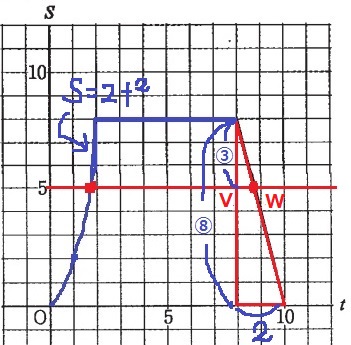
１つ目は、Ｓ＝２ｔ²のところ。
５＝２ｔ²
ｔ＝±√（５/２）＝±√10/２
ｔ＞０より、ｔ＝√10/２

２つ目は、三角形の相似を用いる。
ＶＷ＝２×３/８＝３/４
Ｗのｔ座標は、８＋３/４＝35/４
したがって、ｔ＝√10/２、35/４

大問６（関数）

（１）　79.7%
ｙ＝ｘ－１にｙ＝０を放り込む。
０＝ｘ－１
ｘ＝１

（２）　64.0％
２直線の交点座標は方程式で解く。
ｘ－１＝１/３ｘ＋３
ｘ＝６

ｙ＝６－１＝５
Ｐ（６、５）

（３）　60.9％
Ａ（1、０）Ｂ（０、３）
△ＯＡＢで三平方。
ＡＢ＝√（１²＋３²）＝√10

（４）　19.8％！（部分点14.7％）
∠ＡＢＰ＝90°となる理由。
誘導があるのでありがたい。三平方の定理が成り立てばいい。

長方形を描くとわかりやすいかな？
ＢＰ＝√（６²＋２²）＝２√10
ＰＡ＝√（５²＋５²）＝５√２

ＡＢ＝√10なので、
√10²＋２√10²＝５√２²
すなわち、ＡＢ²＋ＢＰ²＝ＰＡ²という関係が成り立つので、
ＰＡを斜辺、その反対側にある∠ＡＢＰ＝90°となる直角三角形。

（５）　2.0％!!（無答73.6％）
まずは図形を確認。

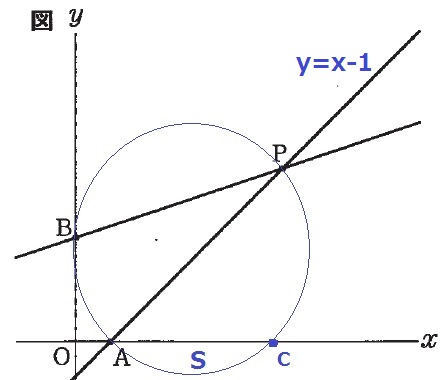
問題文からＣとＳの位置を確定する。
Ｃの座標を決めたい。
ＡＰが円の直径である点に注目。

直径に対する円周角は90°。
また、ｙ＝ｘ－１は傾きが１なので45度線。
ここから、△ＡＣＰは45°－45°－90°の直角二等辺三角形となる。
Ｃ（６、０）

ＣからＡＰに向けて垂線をひくと、円の中心であるＯと交わる。
なぜなら、∠ＯＡＣ＝45°であり、傾き１に対して直交する線分の傾きは－１、
つまり、45度に傾くので、45°－45°－90°の直角二等辺（ＯＡ＝ＯＣ；円の半径）になるから。
１：１：√２より、ＯＡ＝ＯＣ＝５×１/√２＝５√２/２

Ｓを回転させたときの立体を想像する。
求めるべき立体は、半球から内部の円錐をひく。
球の体積：４/３πｒ³
半球－円錐
＝４/３π×（５√２/２）³×１/２－（５√２/２）²π×５√２/２×１/３
＝（５√２/２）³π×２/３－（５√２/２）³π－１/３
＝（５√２/２）³π×（２/３－１/３）
＝125√２/４π×１/３
＝125√２/12πｃｍ³
式が複雑で計算力も問われる(;`ω´)
分配法則をうまく利用しよう。
公立高校入試解説ページに戻る