問題はコチラ→ＰＤＦファイル
大問１（計算）
（ア）
－11＋（－５）
＝－11－５
＝－16 【１】
（イ）
１/５－９/10
＝－７/10 【２】
（ウ）
（５ｘ－ｙ）/６－（３ｘ－４ｙ）/８
＝｛４（５ｘ－ｙ）－３（３ｘ－４ｙ）｝/24
＝（20ｘ－４ｙ－９ｘ＋12ｙ）/24
＝（11ｘ＋８ｙ）/24 【４】
（エ）
25/√10－√40＋√５/√２
＝５√10/２－２√10＋√10/２
＝√10 【２】
（オ）
（ｘ＋９）（ｘ－６）－（ｘ－４）2
＝ｘ2＋３ｘ－54－ｘ2＋８ｘ－16
＝11ｘ－70 【３】
大問２（小問集合）
（ア）
５ｘ＋８ｙ＝－２ …①
１/３ｘ＋３/４ｙ＝－１ ←12倍
４ｘ＋９ｙ＝－12 …②
数字の並びが(;´･ω･)
②×５－①×４をすると、
13ｙ＝－52
ｙ＝－４
①に代入、５ｘ－８×（－４）＝－２
５ｘ＝30
ｘ＝６
ｘ＝６、ｙ＝－４ 【４】
（イ）
２ｘ2－８ｘ＋１＝０
解の公式を適用して、ｘ＝（４±√14）/２ 【４】
（ウ）
ｙ＝ａｘ2において、ｘの値がｐ→ｑに増加したときに変化の割合はａ（ｐ＋ｑ）。
一次関数の変化の割合は傾きで表される。
ａ（１＋３）＝－６
４ａ＝－６
ａ＝－３/２ 【１】
（エ）
加えた食塩水をｘｇとする。
食塩の量で等式を立てる。
350×0.05＋0.15ｘ＝（350＋ｘ）×0.08 ←100倍
1750＋15ｘ＝2800＋８ｘ
７ｘ＝1050
ｘ＝150→150ｇ 【２】
＠別解＠
中学受験では天秤法というテクニックがあります。
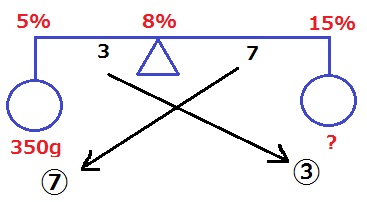
混ぜた後の濃度８％を支点にする。
支点からの距離は３：７。
天秤が釣り合うには、重さを逆比にして⑦：③。
350×③/⑦＝150ｇ
（オ）
整数になる→根号が外れる→根号の中身は平方数。
61までの平方数は、【１、４、９、16、25、36、49】の７個。
４の倍数＋１から４の倍数を引いた数は、４の倍数＋１である。
条件に合う平方数は、【１、９、25、49】の４個。 【３】
（具体的にいうと、ｎ＝３、９、13、15）
大問３（小問集合２）
（ア）ⅰ
△ＡＥＦ≡△ＢＤＥの証明。
仮定より、∠ＥＡＦ＝∠ＤＢＥ（●）
ＡＢ＝ＡＣでＤとＥは各々の中点だから、ＤＢ＝ＡＥ
△ＡＤＥは二等辺三角形で底角が等しいので、∠ＡＤＥ＝∠ＡＥＤ（×）
△ＡＤＥに外角定理を適用、∠ＡＥＦ＝∠ＡＤＥ（×）＋∠ＤＡＥ（▲）
∠ＢＤＥ＝∠ＡＥＤ（×）＋∠ＤＡＥ（▲）
∠ＡＥＦ＝∠ＢＤＥ
（もしくは、180－×で等角と指摘してもよい）
以上より、１辺と両端角が等しいので合同。
ａ…【３】、ｂ…【１】
ⅱ
ＧＥ：ＥＨを求めたい。
ＧとＨが垂線上にあるので、直角をどこかで使わなくてはならない。
△ＡＢＣは二等辺三角形。二等辺で直角といえば底辺の垂直二等分線！
底辺ＢＣの垂直二等分線をひき、ＤＦ、ＢＦ、ＢＣとの交点をそれぞれＩ、Ｊ、Ｋとする。
△ＧＨＦ∽△ＡＪＦに着目してＩＦを境に上下を観察すると、ＧＥ：ＥＨ＝ＡＩ：ＩＪである。
（△ＧＥＦ：△ＡＩＦ＝△ＨＥＦ：△ＪＩＦ）
ＡＩ：ＩＪを求めれば良い。
何ら長さの情報が与えられていない。そこで等辺から見当をつける。
ＤＩ＝ＩＥ＝●とする。
△ＡＤＥ∽△ＡＢＣ、ＫはＢＣの中点だから、ＢＫ＝ＫＣ＝●●
前問の合同より、ＤＥ＝ＥＦ＝●●
△ＢＫＪ∽△ＦＩＪの相似比で、ＩＪ：ＪＫ＝③：②
△ＡＤＥ∽△ＡＢＣ→ＡＩ＝ＩＫ＝⑤
ＡＩ：ＩＪ＝ＧＥ：ＥＦ＝５：３ 【３】
（イ）
クセがある。
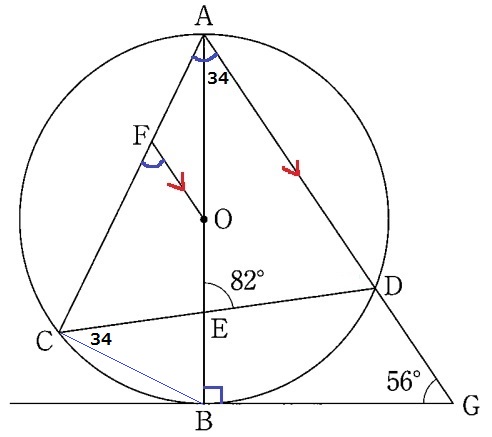
ＡＤ//ＦＯより、同位角で∠ＯＦＣ＝∠ＤＡＦ
∠ＤＡＦを求めれば良い。
直径ＡＢと接線ＢＧは直交するから、∠ＡＢＧ＝90°
△ＡＢＧの内角から、∠ＧＡＢ＝180－（90＋56）＝34°
ＣＢに補助線をひく。
弧ＢＤに対する円周角より、∠ＢＣＤ＝34°
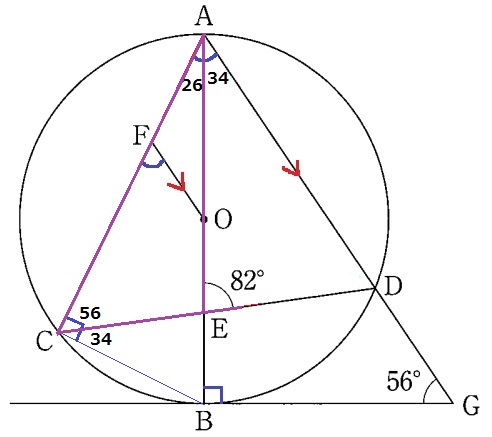
直径ＡＢに対する円周角から∠ＡＣＢ＝90°
∠ＡＣＥ＝90－34＝56°
△ＡＣＥで外角定理→∠ＣＡＥ＝82－56＝26°
∠ＤＡＦ（∠ＯＦＣ）＝26＋34＝60°
（ウ）
Ⅰ：12ヶ月の第１四分位数は下から３番目と４番目の平均。
地点Ａの第１四分位数が20℃超え→少なくとも９ヶ月は20℃以上。〇
Ⅱ：地点ＢとＣの30～35℃を見ると、Ｃは中央値から最大値までスッポリ含まれる。
Ｃの半分（６ヶ月）は少なくとも30～35℃の範囲に入る。ＢよりＣの方が多い。〇
Ⅲ：四分位範囲＝第３四分位数－第１四分位数。箱の横の長さでＥよりＤの方が大きい。×
Ⅳ：最大値が30℃以上なので正しい。〇
Ⅴ：地点Ｅは中央値が25℃を下回る。25℃以上は最大でも６か月。×
確実に読み取れるのはⅠ、Ⅱ、Ⅳ。 【５】
（エ）
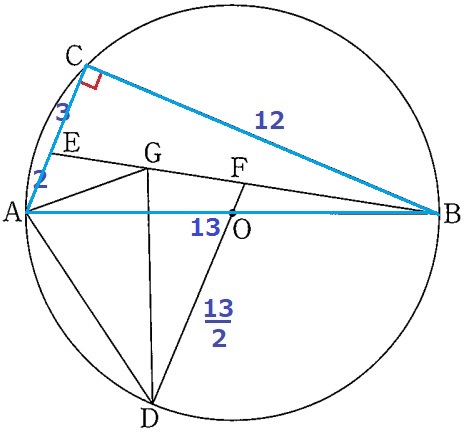
直径に対する円周角→∠ＡＣＢ＝90°
５：12：13の直角三角形は覚えておこう。ＡＣ＝５ｃｍ
ＡＥ：ＥＣ＝２：３より、ＡＥ＝２ｃｍ
直径ＡＢ＝13ｃｍから半径ＤＯ＝13/２ｃｍ
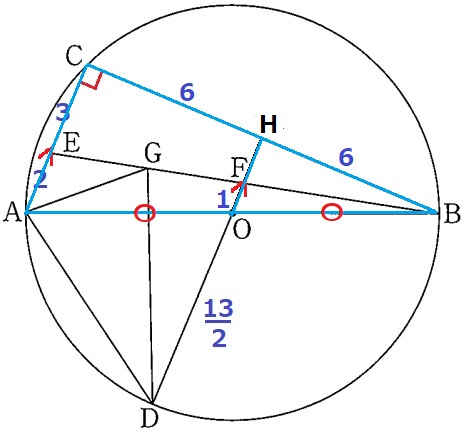
ＯＦを延長、ＣＢとの交点をＨとする。
ＡＣ//ＯＨから、ＡＯ：ＯＢ＝ＣＨ：ＨＢ＝１：１
ＨはＣＢの中点でＣＨ＝６ｃｍ
また、△ＡＢＥ∽△ＯＢＦの相似比は２：１→ＯＦ＝１ｃｍ
四角形ＡＤＦＥは台形。
△ＡＤＥ：△ＡＤＦ＝ＡＥ：ＤＦ＝２：15/２＝④：⑮
王道の解き方ではないかもしれぬが(;`ω´)、ここで面積の変化率を使います。
ＥからＦに点が動くとする。
スタートのＥでは④（△ＡＤＥ）、ゴールのＦでは⑮（△ＡＤＦ）。
底辺をＡＤとすると高さの比は一定の割合で上昇するので、面積の変化率も一定。
ＧはＥＦの中点だから△ＡＤＧの面積は△ＡＤＥと△ＡＤＦの平均→（④＋⑮）÷２＝〇19/２
△ＡＤＥの面積は２×６÷２＝６ｃｍ2なので、△ＡＤＧ＝６×(〇19/２)/④＝57/４ｃｍ2
大問４（関数）
（ア）
ｙ＝ａｘ2上にあるＡ座標に着目する。
ｙ＝－ｘ＋２にｘ＝－６を代入する。Ａ（－６、８）
これをｙ＝ａｘ2に代入。
８＝36ａ
ａ＝２/９ 【２】
（イ）
ｙ＝８/ｘにｘ＝２を代入→Ｅ（２、４）
Ｆは原点ＯについてＥと対称→Ｆ（－２、－４）
ＣＯ：ＯＤ＝３：４より、Ｄのｘ座標は８。
Ｆから右に10、上に４でＤだから、傾きｍは４/10＝２/５
切片ｎはＦから右に⑤（＝２）、上に②進んで、ｎ＝－４＋２×②/⑤＝－16/５
ⅰ…【２】、ⅱ…【１】
（ウ）
イカニモ神奈川(´Д`川)
各頂点の座標を記しておく。
Ｇはｙ＝－ｘ＋２とｙ＝２ｘの交点。
－ｘ＋２＝２ｘ
ｘ＝２/３→Ｇ（２/３、４/３）
ＥＧ：ＧＦ＝４/３：８/３＝１：２
試しにＡＧとＦＤの交点を求めてみると、ｘ＝26/７と容赦ない数字が現れる(;°;ω;°;)
四角形ＡＢＦＧと△ＤＥＧは離れており、形も美しくない…。
なるべく点座標や直線の式が整数であるところを利用したい。
Ｄを通るＥＦに平行な線をひき、ＡＧとの交点をＨとする。
ＤＨの傾きは２。（８、０）を通るのでｙ＝２ｘ－16
Ｈのｘ座標は、－ｘ＋２＝２ｘ－16
ｘ＝６→Ｈ（６、－４）
ＦＨはｘ軸と平行である。
等積変形で、△ＤＧＦ＝△ＨＧＦ、△ＤＥＧ＝△ＨＥＧ
ＡＦに補助線。
△ＡＧＦ：△ＨＧＦ＝ＡＧ：ＧＨ＝20/３：16/３＝⑤：④
ＥＧ：ＧＦ＝１：２から、△ＨＥＧ＝②
残りは△ＡＢＦ…。
ここまでくれば地道に面積を求めてもよいのですが、面積比を続けます。
ＡＢとＨＦを延長、交点をＩとする。
ＩＦ：ＦＨ＝４：８＝①：②
ＡＢ：ＢＩ＝28/３：８/３＝⑦：②
△ＡＦＨ＝⑨なので、△ＡＢＦ＝⑨×①/②×⑦/⑨＝〇3.5
四角形ＡＢＦＧ：△ＤＥＧ（△ＨＥＧ）＝〇8.5：②＝17：４
良い解法を編み出した方は下のコメント欄かお問い合わせよりお知らせ願いますm(_)m
ちなみに、ＢＦとＥＤは平行ですが、いまいち活用法を見出せませんでした。
＠別解＠
ぶんちんさんから素敵な別解を頂きました(*´д`艸)
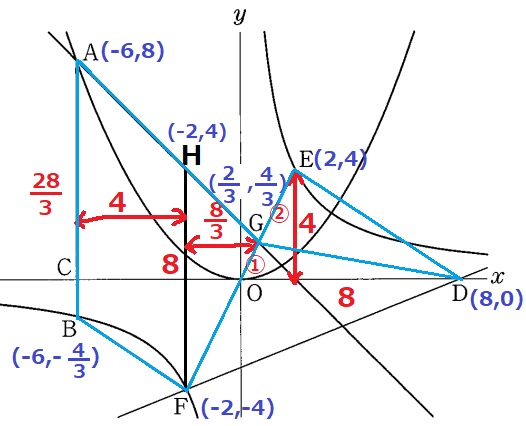
Ｆを通るｙ軸に平行な線を引き、ＡＧとの交点をＨとします。
ｙ＝－ｘ＋２にｘ＝－２を代入→Ｈ（－２、４）
四角形ＡＢＦＧは台形ＡＢＦＨと△ＨＦＧに分割されます。
△ＤＥＧは△ＯＤＥから△ＯＤＧを引けば良いので、
ＯＧ：ＯＥ＝２/３：２＝①：③→△ＤＥＧ＝△ＯＤＥ×②/③から求められます。
必要な数値は上図の通り。
四角形ＡＢＦＧ＝（28/３＋８）×４÷２＋８×８/３÷２＝104/３＋32/３＝136/３
△ＤＥＧ＝８×４÷２×②/③＝32/３
四角形ＡＢＦＧ：△ＤＥＧ＝136/３：32/３＝17：４
こちらの解法の方が現実的かと思います。
＠別解２＠
しやばこさんから貴重なタレコミを頂きました(*´ω`*)
ＢＧとＦＤはともに傾き２/５の平行で、四角形を三角形に置き換えることができます。
これを使って、サボなりに別の解法をつくってみました。
ＦＧ；ｙ＝２/５ｘ－16/５
ｙ＝－ｘ＋２とＦＤの交点をＨとすると、Ｈのｘ座標は26/７。
四角形ＡＢＦＧを△ＡＢＨに変形します。
Ｆ→Ｈとｙ＝－ｘ＋２に乗っけたので、Ｄも乗っけます。
先のようにＤを通るＥＦに平行な線をひき、交点をＩとするとＩのｘ座標は６。
また、Ｅから垂線を下ろすと、ｘ軸との交点（２、０）はｙ＝－ｘ＋２にあります。
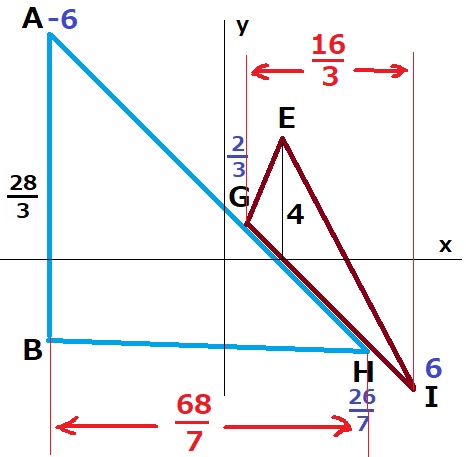
必要な数値を抜き出します。
△ＡＢＨ：△ＩＥＧ＝28/３×68/７：４×16/３
＝17：４
大問５（確率）
（ア）
●条件整理●
操作１：Ｐ→Ｑ（＝ＰからＱに移す）
操作２：Ｐ≧ＱのときはＰ→Ｑ、Ｐ＜ＱのときはＱ→Ｐ
操作１でＰを６個以下にしないと、操作２でＰを０個にできない。
また、操作２でＰ→ＱとなるギリギリのラインはＰ＝Ｑ
玉は合計12個だから（Ｐ、Ｑ）＝（６、６）である。
ということは、操作１終了後のＰは６個しかない。
操作１で（Ｐ、Ｑ）＝（６、６）、操作２で（０、12）
全体は６×６＝36通り、場合の数は１通りだから確率は１/36。
（イ）
操作２において、Ｐ→ＱかＱ→Ｐで場合分けする。
最終的にＰ＞Ｑなので、Ｐは７個以上、Ｑは５個以下になる。
◆Ｐ→Ｑ
初期状態は（Ｐ、Ｑ）＝（９、３）
操作１で１個移して（８、４）、操作２で１個移して（７、５）
この１通りしかない。
◆Ｑ→Ｐ
操作１終了後はＰ＜Ｑ、（Ｐ、Ｑ）＝（５、７）（４、８）（３、６）の３通り。
操作２終了後のＰは７個以上だから、（５、７）はＰの個数が＋２～６の５通り。
（４、８）はＰが＋３～６の４通り、（３、６）はＰが＋４～６の３通り。
合計すると13通りで、確率は13/36。
大問６（空間図形）
（ア）
底面は１辺６ｃｍの正方形。
４つの側面を伸ばすと、縦５ｃｍ、横６×４＝24ｃｍの長方形。
表面積は、６×６×２＋24×５＝192ｃｍ2 【４】
（イ）
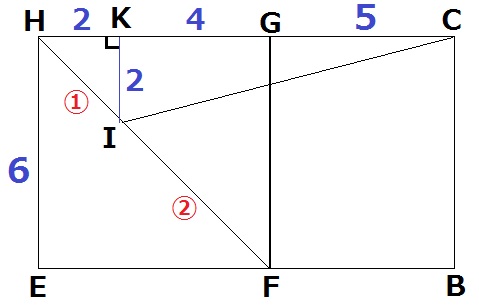
展開図をつくる。
求めたいＩＣを斜辺とする直角三角形で三平方の定理を使いたい。
そこで、ＩからＨＣに垂線をひいて交点をＫとし、△ＫＩＣをつくる。
△ＨＩＫ∽△ＨＦＧより、ＨＫ：ＫＧ＝１：２→ＫＧ＝６×２/３＝４ｃｍ
ＫＩ：ＧＦ＝１：３→ＫＩ＝６×１/３＝２ｃｍ
（△ＨＩＫは直角二等辺三角形である）
△ＫＩＣで三平方→ＩＣ＝√85ｃｍ 【３】
（ウ）
線分ＦＪを含む面ＨＤＢＦで切り取る。
△ＥＦＨは直角二等辺三角形→ＨＦ＝６√２ｃｍ
ＨＩ：ＩＦ＝①：②より、ＨＩ＝２√２ｃｍ、ＩＦ＝４√２ｃｍ
正方形の対角線ＡＣとＢＤの交点Ｏはおのおのの中点なので、ＤＯ＝ＯＢ＝３√２ｃｍ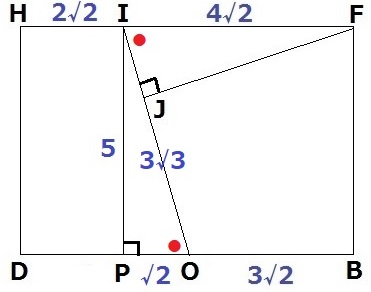
ＩからＤＢに垂線をひき、足をＰとする。
ＰＯ＝３√２－２√２＝√２ｃｍ
ＨＦ//ＤＢより錯角で∠ＩＯＰ＝∠ＦＩＪ（●）、２角相等で△ＩＰＯ∽△ＦＪＩ
△ＩＰＯで三平方→ＩＯ＝３√３ｃｍ
ＩＰ：ＩＯ＝ＦＪ：ＦＩなので、
ＦＪ＝４√２×５/３√３＝20√６/９ｃｍ
取るべきところは取る、捨てるところは捨てる、
といった戦略的な取捨選択が合否を分けるいつもの神奈川。
大問１
満点かつ迅速に終わらす。
大問２
ここまでは取りたい。１と２で配点35点。
（ア）他とのバランスから、もう少しやりやすい係数にしてあげて(;´･ω･)
（エ）天秤法に甘えてしまった。
（オ）過去問の踏襲。
大問３
（ア）ⅰ：手順が多いので、いちいち全部読んでいる暇はない。
空欄の前後読みで対処する。
ⅱ：Ａからの垂線をひけないと迷子。
ＤＦ⊥ＧＨから垂直をどこかでつくり、ＧＥ：ＥＨを別の辺の比に移す。
辺の長さがわからないので、等辺と合同を利用して相似比を計算する。
（イ）変な場所にある∠ＯＦＣを早々と∠ＤＡＦに移動させる。
Ｅは円周上の点ではない→82°は対頂角か外角定理で使うしかない。
直径に対する円周角をどこかに作る。
（ウ）内容は難しくないが、５つの要素を手際よく判断したい。
（エ）発想系というよりテクニカルな設問であった。
テクニックは塾で習ってください。
大問４
（ウ）神奈川色が強め。分割して求めていくのが手堅いかと。。
せめてＢ座標は整数値であれ(#`Д´)ﾉﾉ┻┻
処理能力も問われ、間違ったルートを選んでやり直しだと心が折れる。
解説では△ＨＧＦを媒介に３つの三角形の面積比を求めた。
ＢＦ//ＥＤを活用した解法がございましたら教えてください。
大問５
確率は良問であった。
いくつかの問題をスキップして、ここで調べる時間に費やすのが得策か。
条件の把握も的確かつなるべく迅速に。
（ア）思考力が試される。
移動できる玉の個数は１～６個。Ｐの個数は９→６→０しかない。
（イ）操作２で分岐があるので、操作２の内容で分けてみる。
大問６
（イ）他県でも見かけるパターンだが正答率は低い。ナナメ線は三平方。
（ウ）ＦＪは三角錘Ｆ―ＩＡＣの高さだが、体積が求めづらい。
ＪＦが面ＨＤＢＦ上にあることから、△ＦＪＩと相似にある三角形を面上に作れないか。
＠2023年度・神奈川解説＠
数学…平均53.0点 社会…平均58.4点 理科…平均51.0点 英語…平均55.3点
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント
神奈川県追試験問4ですが、
ＢＧとＦＤが平行になるので、△ＧＢＦを等積変形してＢＯＨ（Ｈは①とＤＦの交点）にして求めると面積１つでできて楽かもしれません。
コメントありがとうございます。
よく見つけましたね！
ＢＧとＦＤがともに傾き２/５は気づかなかったです。
あれこれ考えてみたのですが、ＡＢ＝28/３とＧ座標は必要っぽいので、
せめてＨのｘ座標くらいは整数にしてくれたら良かったんですけどね(;^ω^)
せっかく頂いたご意見なので、自分なりにトライして後ほど掲載したいと思います。
ありがとうございます。
サボ