問題はこちら→東進ハイスクールさん(解答)
大問1(小問集合)
(1) 89.4%
3-(-5)
=3+5
=8
(2) 77.3%
8a3b2÷6ab
=4/3a2b
(3) 89.4%
(x+3)2
=x2+6x+9
(4) 54.1%
パンが7x円、ジュースが5y円、合計が2000円以下。
7x+5y≦2000
(5) 69.1%
ねじれの位置…延長しても交わらない、かつ平行でもない。
辺DH、辺CG、辺EH、辺FGの4本。
(6) 61.8%
反比例の比例定数aはxとyの積で一定。
a=-2×8=16
y=-16/x
(7) 47.8%
360-134=226°
円周角の定理より、x=226÷2=113°
(8) 35.5%
面積比は相似比の2乗。
△ABC:△DEF=32:52=9:25
△DEFの面積は△ABCの25/9倍。
大問2(小問集合2)
(1) 56.2%
x2+4x+1=0
解の公式を適用。xの係数が偶数なのでb=2b’が使える。
x=-2±√3
(2) 12.8%!(部分正答含34.4%)
答案では、使用できる教室の数をxとして方程式をつくり、途中の計算も書く。
生徒の人数で等式を立てる。
1教室に15人ずつ入れると34人が入れない→15x+34人
1教室に20人ずつ入れると14人の教室が1つ、空き教室が1つできる。
→20x人から6人不足、さらに20人不足→20x-6-20人
15x+34=20x-6-20
5x=60
x=12
使用できる教室の数は12
(3) 8.0%!!(部分正答含54.8%)
一の位が0でない900未満の3桁の自然数Mの百の位がa、十の位がb、一の位がc。
1≦a≦8、0≦b≦9、1≦c≦9
M=100a+10b+c
N=M+99
=100a+10b+c+100-1
=100×(a+1)+10×b+c-1
Nの百の位はa+1、十の位はb、一の位はc-1となる。
よって、Mの位の数の和とNの位の数の和は、それぞれa+b+cで同じ値になる。
①…100、②…10、③…a+1、④…b、⑤…c-1
@@
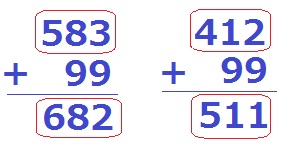
比較すると、一の位が-1、十の位は変化なし、百の位は+1で和は変わりません。
大問3(平面図形)
(1) 19.3%!

①ABを1辺とする正三角形をつくる。
②角の二等分線で60°を2等分すれば30°がつくれる。
ACとの交点がP。
(2)① 56.0%

Aから垂線をひき、DCとの交点をEとする。
EC=AB=2cm、DE=3-2=1cm
△AEDで三平方→AD=√10cm
② 43.1%
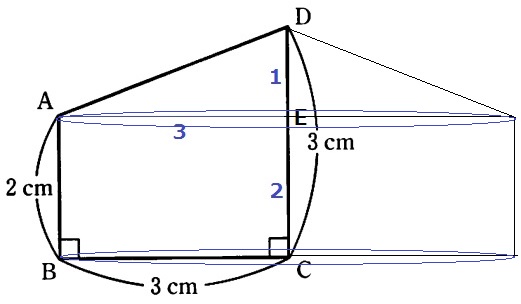
回転体は下が円柱、上が円錐。
3×3×π×2+3×3×π×1÷3
=21πcm3
(3) 4.6%!!(部分正答71.5%)
△ABF≡△DAGの証明。
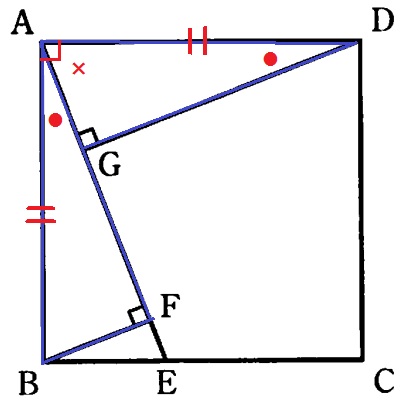
仮定より、∠BFA=∠AGD=90°
AB=DA
∠BAF(●)=90-∠DAG(×)
△DAGの内角で、∠ADG=180-(90+×)=90-×=●
斜辺と1つの鋭角が等しい直角三角形だから合同。
大問4(データの活用)
(1) 65.4%
選ばれるのは5人中2人なので、確率は2/5。
Aが選ばれるのもCが選ばれるのも、みな同様に確率は2/5。
(2)① 36.3%
累積度数は、その階級以下の度数の和。
2+7+8=17人
② 62.2%
最頻値(モード)は最もあらわれている値。
20.0~22.0の階級に含まれる→階級値は21.0秒
(3)① 77.4%
ア:中央値(第2四分位数)は1回目が13点、2回目が14点。〇
イ:最大値は1回目が18点、2回目が20点。×
ウ:範囲=最大値-最小値。1回目は18-6=12点、2回目は20-8=12点。×
エ:四分位範囲=第3四分位数-第1四分位数。箱の長さで2回目の方が小さい。〇
1回目は16-8=8点、2回目は16-10=6点
ア・エ
② 11.2%!(部分正答23.4%)
説明問題。
100人の第1四分位数は25番目と26番目の平均。
たとえば、25番目が7点、26番目が9点だった場合、
8点の生徒がいなくても第1四分位数は8点になる。
25番目が6点、26番目が10点なども同様である。
大問5(関数・数量変化)
(1)① 56.7%
x=0のとき、最小値y=0
x=5のとき、最大値y=50
0≦y≦50
② 17.1%!
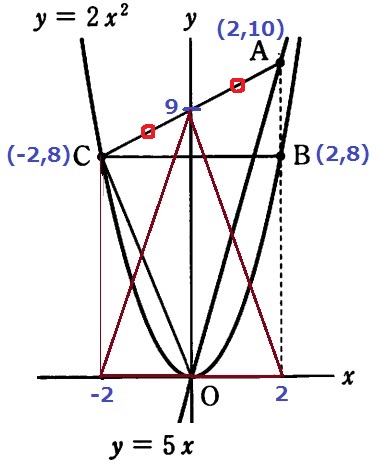
y=5x、y=2x2にそれぞれx=2を代入。
A(2、10)B(2、8)
Cはy軸についてBと対称。C(-2、8)
直線CAの切片はCとAの中点から(0、9)
等積変形の考えで、△OACは底辺4、高さ9の三角形。
4×9÷2=18
③ 3.8%!!(部分正答含11.7%)
答案では途中の計算も書く。
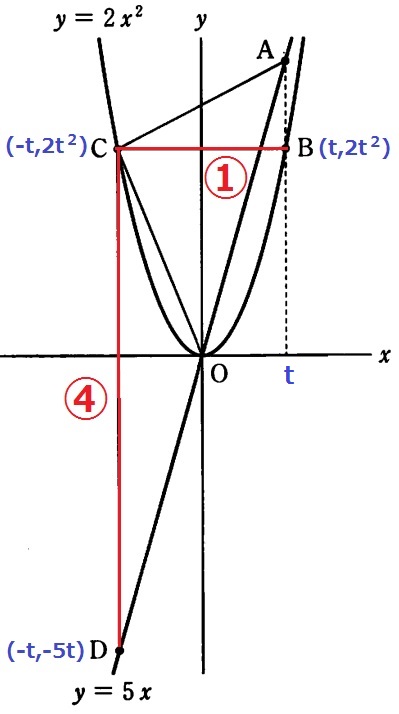
座標をtで表す。
y=2x2にtを代入。B(t、2t2)
Cはy軸についてBと対称。C(-t、2t2)
y=5xにx=-tを代入。D(-t、-5t)
BC=t-(-t)=2t
CD=2t2-(-5t)=2t2+5t
4BC=CDだから、4×2t=2t2+5t
2t2-3t
=t(2t-3)=0
t>0より、t=3/2
(2)① 75.0%
390m÷6分=毎分65m
② 22.0%!(部分正答含34.9%)
答案では途中の計算も記述する。
グラフの横軸が時間、縦軸が距離だから、傾きが速さになる。
前田の速さは毎分70m→傾きは70
y=70x+bに(6、390)を代入する。
390=70×6+b
b=-30
y=70x-30
③ 1.2%!!
情報整理が求められる。

図書館の280m手前で、後藤が前田に追いつく。
29分から280÷70=4分前→25分のとき
後藤家~前田が後藤に追いつかれる地点までの2人の移動距離は同じ。
前田の移動時間は、8+6=14分間
速さの比が、前田:後藤=70:210=1:3
時間の比は逆比で、前田:後藤=3:1
⇒後藤の移動時間は、14÷3=14/3分=4分40秒
後藤が家を出発したのは家に着いてから、
25分-6分-4分40秒=14分20秒後
大問6(方程式)
(1) 63.3%
マスの数は、4×4=16個
白は1マス4枚貼るから、4×16=64枚
(2) 24.1%!(部分正答含30.8%)
黒のマスをx個、白のマスをy個とする。
n=5のとき、マスは全体で5×5=25個
x+y=25 …①
もう1つは、タイルの枚数の合計で等式。
x+4y=49 …②
①-②より、3y=24
y=8
白マスは8個。白のタイルは4×8=32枚
①にy=8を代入して、黒のマスは25-8=17個→黒のタイルは17枚
黒いタイル…17枚、白いタイル…32枚
(3) 0.1%!!!(部分正答含6.2%)
n=aのとき、マスは全体でa2個。
黒マスがb個、白マスはa2-b個。
→黒のタイルはb枚、白のタイルは4(a2-b)枚。
貼り方のⅠとⅡを逆にした⇒黒と白のタイルを入れ替えた。
黒マスはa2-b個、白マスはb個。
→黒のタイルは(a2-b)枚、白のタイルは4b枚。
b+4(a2-b)=(a2-b)+4b+225
3a2-6b=225 ←÷3
a2-2b=75
a2=2b+75
ここで偶奇判定。
2bは偶数、75は奇数なので、a2は奇数でなければならない。
a2が奇数ということは、aは奇数。(奇数×奇数=奇数)
問題文より、aは2以上の整数、bは1以上の整数で、
a2は77以上の奇数の平方数が該当する。
9×9=81→aの最小値は9。その次の奇数は11。
①…4(a2-b)、②…9、③…11
●講評●
変わった設問も見受けられるが、全体的に典型問題の割合が高い。
大問1
基本。全部とろう。
大問2
(2)20x人から何人不足しているか。
(3)やや特殊な設定だが、素直に誘導に従うと解きやすい。
99=100-1に分け、100をaに持っていく。
(a+1)+b+(c-1)=a+b+cで位の和が等しくなる。
大問3
問題集や模試に出てきそうな典型題がつづく。
大問4
ここも取りやすかった。
(3)②(〇+〇)÷2=8、(8、8)以外の組み合わせを書く。
大問5
(1)②CAの切片→CAの中点。
③初手は座標をtで表す。標準レベル。
(2)③解法によって時間差が生まれやすい。
前問の式を使わないほうが早いと思う。
まず、前田と後藤の速さの比がちょうど1:3であることに気がつきたい。
求めたいのは後藤が家に滞在していた時間。
後藤家から図書館の280m手前まで、前田と後藤は同じ距離を移動している。
距離一定ならば、移動時間の比は速さの逆比。後藤は25分のときに追いつく。
それまでの前田の移動時間から後藤の移動時間がわかる。
大問6
(2)マスの個数とタイルの枚数は分けて考える。
(3)aとbの関係を簡潔な式にまとめる。
aの最小値を求めるには、aの条件を定める。ここで偶奇判定を使う。



コメント