2021年度　東京都立高校入試問題過去問【数学】解説

平均53.3点（前年比；－7.8点）

問題はコチラ→ＰＤＦファイル
2021年度・都立分割後期（数学）の解説はコチラ。
出題範囲の除外は三平方の定理と標本調査。

大問１（小問集合）－66.1％

（１）　88.3％
－３²×１/９＋８
＝－１＋８＝７

（２）　62.0％
（５ａ－ｂ）/２－（ａ－７ｂ）/４
＝｛２（５ａ－ｂ）－（ａ－７ｂ）｝/４
＝（９ａ＋５ｂ）/４
*誤答は９ａ+５ｂが多かった。

（３）　55.3％
３÷√６×√８

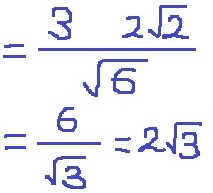
２√３
*√８＝２√２に変換して、根号同士で約分。
誤答は√３/４、４√３/３が多かった。

（４）　84.6％
－４ｘ＋２＝９（ｘ－７）
－４ｘ＋２＝９ｘ－63
13ｘ＝65
ｘ＝５

（５）　87.7％
５ｘ＋ｙ＝１　…①
－ｘ＋６ｙ＝37　…②
サボは①×６－②でやりました。
31ｘ＝－31
ｘ＝－１
①に代入。－５＋ｙ＝１
ｙ＝６
ｘ＝－１、ｙ＝６

（６）　54.8％
（ｘ＋８）²＝２
ｘ＋８＝±√２
ｘ＝－８±√２

（７）　56.2％
傾きが負だから、上に凸のグラフ。
ｘ＝０のとき、最大値ｙ＝０
ｘ＝－４のとき、最小値ｙ＝－３×（－４）²＝－48
①…ア、②…オ

（８）　46.6％

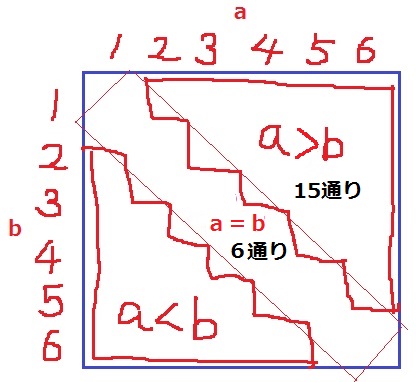
↑頭のなかでこれをイメージする。
ａとｂが同じ目になるのは６通り。
ａ＞ｂは、１＋２＋３＋４＋５＝15通り
計21通り、確率は21/36＝７/12
あ…７、い…１、う…２

（９）　59.1％

２直線から等距離→角の二等分線
２本の二等分線の交点がＰとなる。

大問２（式の証明）－26.1％

（１）①　37.8％

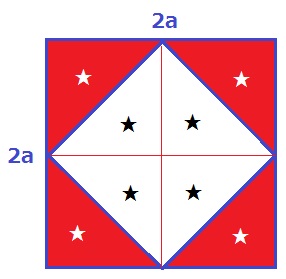
このように分割すると、色がついた部分の面積は正方形の半分。
２ａ×２ａ÷２＝２ａ²
これが５×５＝25枚並ぶので、２ａ²×25＝50ａ²
イ

②
考え方は先ほどと同じ。
１辺の長さが２ａ×５＝10ａなので、
10ａ×10ａ÷２＝50ａ²
ウ
*結局、面積はどちらも等しい。

（２）　14.4％！
方針は立てやすい。基本形は【正方形－円】

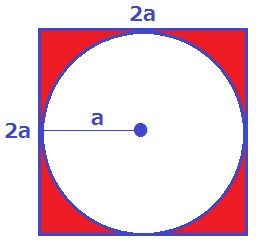
１枚あたりの面積は、２ａ×２ａーａ×ａ×π
＝４ａ²－πａ²＝（４－π）ａ²
これがｎ²枚あるから、Ｘ＝（４－π）ａ²ｎ²

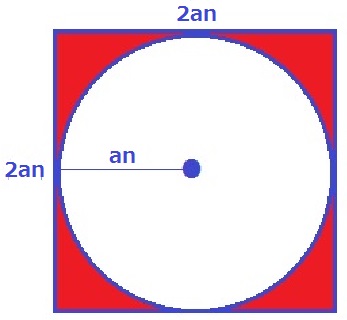
Ｙ＝２ａｎ×２ａｎ－ａｎ×ａｎ×π
＝４ａ²ｎ²－πａ²ｎ²＝（４－π）ａ²ｎ²
Ｘ＝Ｙが導かれた。

大問３（関数）－54.7％

（１）　88.7％
ｙ＝－２ｘ＋14にｙ＝10を代入。
10＝－２ｘ＋14
ｘ＝２
え…２

（２）　65.9％
ｙ＝－２ｘ＋14にｘ＝４を放り込む。
ｙ＝－２×４＋14＝６
Ｐ（４、６）

Ａ（－12、－２）⇒Ｐ（４、６）
右に16、上に８だから、傾きは８/16＝１/２
Ｐ（４、６）から左に４、下に２移動して、切片は６－２＝４
ｍ；ｙ＝１/２ｘ＋４
①…イ、②…ア

（３）　9.3％!!

△ＡＰＢと△ＡＰＱが等積→ＢＱ//ＡＰ
Ｐのｘ座標をｔとすると、Ｐ（ｔ、－２ｔ＋14）

ＡＢの中点をＭ、ＰＱの中点をＮとする。
Ｍ座標はＡとＢの平均→Ｍ（－６、６）
ＰとＱはｘ軸について対称だから、この中点Ｎは（ｔ、０）
ＢＱ//ＡＰということは、各々の中点のＭＮも平行である。

平行線を頼りに、直角三角形の∽を活用する。
Ｍ⇒Ｎは右にｔ＋６、下に６移動する。
Ａ⇒Ｐは右にｔ＋12、下に－２－（－２ｔ＋14）＝２ｔ－16移動する。
（ｔ＋６）：６＝（ｔ＋12）：（２ｔ－16）
外項と内項の積より、
（ｔ＋６）（２ｔ－16）＝６（ｔ＋12）
２ｔ²－４ｔ－96＝６ｔ＋72
２ｔ²－10ｔ－168＝０　←÷２
ｔ²－５ｔ－84
＝（ｔ－12）（ｔ＋７）＝０
ｔ＞７より、ｔ＝12
したがって、Ｐのｘ座標は12。

大問４（平面図形）－32.5％

（１）　64.8％

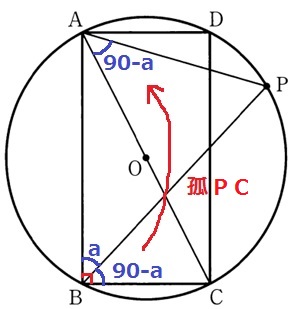
長方形の１つの内角は90°→∠ＰＢＣ＝90－ａ°
弧ＰＣに対する円周角より、∠ＰＡＣ＝90－ａ°
イ

（２）①　32.3％！
△ＱＲＰが二等辺三角形であることの証明。

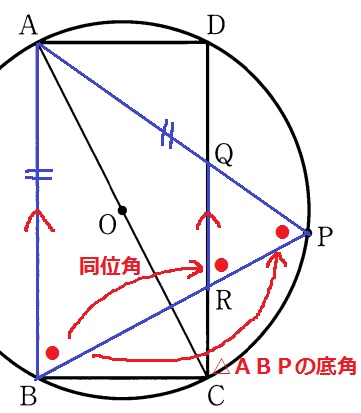
二等辺ということは底角が等しい。
長方形は対辺が平行→ＡＢ//ＤＣの同位角と、△ＡＢＰの底角を合わせると、
∠ＱＲＰ＝∠ＱＰＲとなり、△ＱＲＰは二等辺となる。

②　0.5％!!!（無答37.6％）
三平方が抜かれたので、三平方なしでいきます。

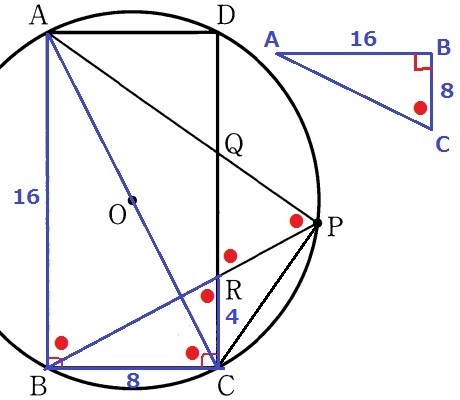
先ほどの等角を利用する。
対頂角で∠ＢＲＣ＝●、孤ＡＢに対する円周角で∠ＡＣＢ＝●
△ＡＢＣと△ＢＣＲに刮目。
●と90°で２角が等しく∽
ＡＢ：ＢＣ＝ＢＣ：ＣＲ＝16：８＝２：１
ＣＲ＝８÷２＝４ｃｍ

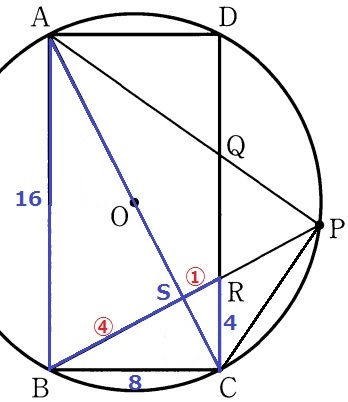
ＡＣとＢＲの交点をＳとする。
平行線と対頂角を頼りに２角が等しく△ＡＢＳ∽△ＣＲＳ
ＢＳ：ＳＲ＝16：４＝④：①

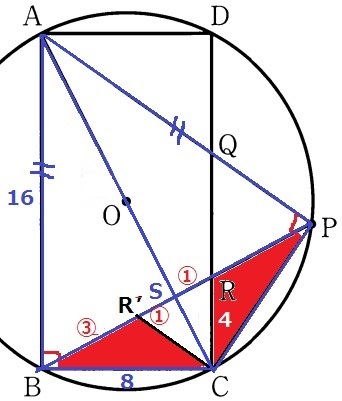
△ＡＢＣと△ＡＰＣはＡＢ＝ＡＰ、半円の弧に対する円周角（直角）、共通辺ＡＣより、
斜辺と他の１辺が等しい直角三角形で合同。
ＡＣを対称の軸とすると、△ＡＢＣ≡△ＡＰＣで左右対称である。
左右対称の図形から上部の二等辺ＡＢＰを取り除いた△ＢＣＳと△ＰＣＳもＳＣを境に対称。
ＡＣについてＲをＢ側へ対称移動させた点をＲ’とおくと、
求積すべき図形は△ＢＣＲ’となる。
ＢＲ’＝ＢＳ－Ｒ’Ｓ＝④－①＝③
【△ＢＣＲ→△ＢＣＲ’】
８×４÷２×③/⑤＝48/５ｃｍ²
お…４、か…８、き…５

大問５（空間図形）－11.9％

（１） 20.2％！
ネジレ→延長しても交わらない、かつ平行でもない。

気をつけるべき点は、ＰＱを延長すると面ＢＣＦＥ上にあるＣＦ・ＢＥと交わること。
ＡＤは面ＢＣＦＥと平行なので、ＰＱと交わらない。
ネジレにある辺は、ＡＣ・ＡＢ・ＡＤ・ＤＦ・ＤＥの５本。
く…５
*７の誤答が多かった。

（２）　3.6％!!

底面は平行四辺形ＢＰＦＱ…４×６＝24ｃｍ²
高さは△ＤＥＦに注目しよう。
ＤからＥＦに向けた垂線の交点をＨとする。
面ＤＥＦと面ＢＣＦＥが垂直ゆえ、ＤＨが立体Ｄ－ＢＰＦＱの高さにあたる。

△ＤＥＦの面積を２通りで表すと、【ＤＥ×ＦＤ÷２＝ＥＦ×ＤＨ÷２】
ＤＨ＝４×３÷５＝12/５ｃｍ
立体ＤーＢＰＦＱの体積は、24×12/５÷３＝96/５ｃｍ³
け…９、こ…６、さ…５

＠2021年度・都立解説＠
数学(分割後期)　社会…平均54.6点　理科…平均47.8点　英語…平均54.1点
公立高校入試解説ページに戻る