2022年度　岩手県公立高校入試問題過去問【数学】解説

平均点57.5点（前年比；＋8.0点）
０～９点…2.8％、10～19点…4.8％、20～29点…7.3％、30～39点…8.5％、40～49点…10.8％
50～59点…13.5％、60～69点…16.2％、70～79点…16.8％、80～89点…12.9％、90～100点…6.3％
問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）　92％
１－（－３）
＝１＋３
＝４

（２）　87％
（15ｘ＋20）÷５　←分配法則
＝15ｘ÷５＋20÷５
＝３ｘ＋４

（３）　79％
５/√２　←分母分子を√２倍
＝（５×√２）/（√２×√２
＝５√２/２

（４）　83％
ｘ²－５ｘ－14
＝（ｘ＋２）（ｘ－７）

（５）　75％
ｘ²－７ｘ＋11＝０
会の公式を適用して、ｘ＝（７±√５）/２

大問２（文字式）

71％
鉛筆３本の代金は３ｘ円、支払ったお金は1000円なので、
おつりｙ円は、ｙ＝1000－３ｘ

大問３（比例）

58％

ｙ＝－１/３ｘのグラフを描く。
（－３、１）、原点、（３、－１）を通過する直線。

大問４（図形）

（１）　57％
体積比は相似比の３乗。
Ｐ：Ｑ＝８：１

（２）　72％

半径でＡＯ＝ＢＯ、二等辺ＡＯＢの底角から∠ＯＡＢ＝30°
弧ＢＣの円周角で、∠ＢＡＣ＝128÷２＝64°
ｘ＝64－30＝34°

（３）　61％

わかりやすかったと思う。
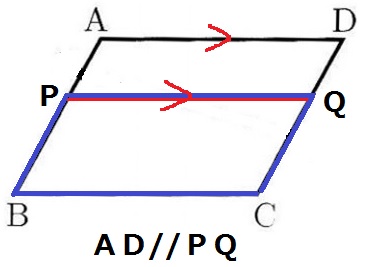
平行四辺形ＰＢＣＱは平行四辺形ＡＢＣＤの高さを短くした感じ。
ＰＱ//ＢＣとＰＢ//ＱＣより、２組の対辺が平行だから平行四辺形である。
イ

他は平行四辺形にならない場合がある。

＠平行四辺形であるための条件＠
①２組の対辺が平行　②２組の対角が等しい　③２組の対辺が等しい
④対角線がおのおのの中点で交わる　⑤１組の対辺が平行で、かつ長さが等しい

大問５（作図）

44％

『２つの半直線ＡＢ、ＡＣから距離が等しい』→∠ＣＡＢの二等分線
これと円Ｏの円周と交わる２つの点が答え。

大問６（データの活用）

71％
ア：６冊以上は１組が12人、２組が８人。×
イ：最頻値（モード）は１組が６冊、２組が４冊。×
ウ：30人の中央値（メジアン）は15番目と16番目の平均。
　１組が５冊で、２組が４冊。〇
エ：ともに30人なので、借りた総数が多いクラスの方が平均値が高い。
　１組…２×４＋３×４＋４×４＋５×６＋６×10＋７×２＝140冊
　２組…２×１＋３×６＋４×10＋５×５＋６×６＋７×２＝135冊×
ウ

＠余談＠

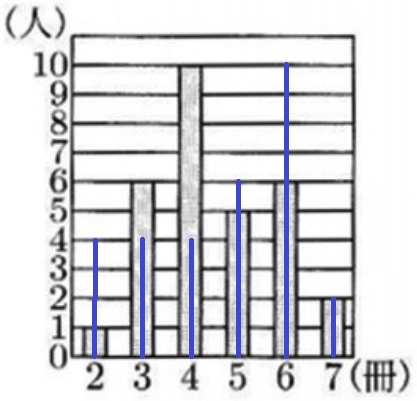
最頻値と中央値がともに１組が大きいので、平均値も大きいと推測できるが、
ヒストグラムに１組のデータを写してみると、あきらかに１組の方が借りている。

大問７（方程式）

48％
答案では用いる文字が何かを示したうえで方程式をつくり、過程を記述する。
50円硬貨をｘ枚とすると、500円硬貨は100－ｘ枚。
50円硬貨の重さは４ｘｇ、500円硬貨の重さは７（100－ｘ）ｇ。

重さで等式を立てると、
４ｘ＋７（100－ｘ）＝804－350
３ｘ＝246
ｘ＝82

50円硬貨は82枚、500円硬貨は100－82＝18枚なので、
50×82＋500×18＝13100円

＠別解＠
もちろん、一次方程式ではなく連立方程式でもできる。
50円硬貨をｘ枚、500円硬貨をｙ枚とすると、
ｘ＋ｙ＝100
４ｘ＋７ｙ＝804－350
これを解くと、ｘ＝82、ｙ＝18

大問８（平面図形）

36％
ＢＨ＝ＧＨの証明。

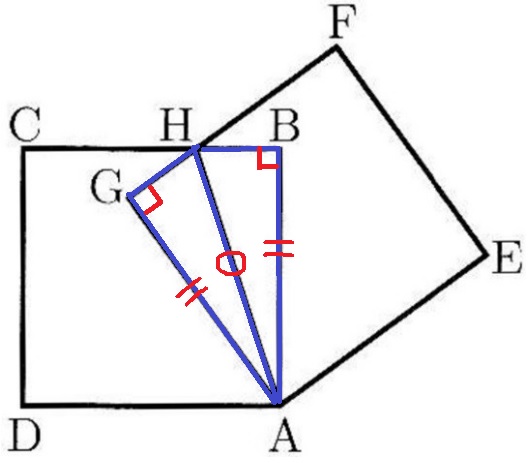
方針は立てやすい。
ＢＨとＧＨを１辺とする合同っぽい三角形→△ＡＢＨ≡△ＡＧＨを証明すればいい。
正方形だからＡＢ＝ＡＧ、∠ＡＢＨ＝∠ＡＧＨ＝90°
ＡＨは共通辺、以上より斜辺と他の１辺が等しい直角三角形だから△ＡＢＨ≡△ＡＧＨ。
対応する辺よりＢＨ＝ＧＨ

大問９（数量変化）

（１）　80％
ｘが「花壇からの距離」で、ｙは「影の長さ」。
ｘ＝４のときのｙ座標の差は、花壇からの距離が４ｍのときの影の長さの差。
エ

（２）　24％！

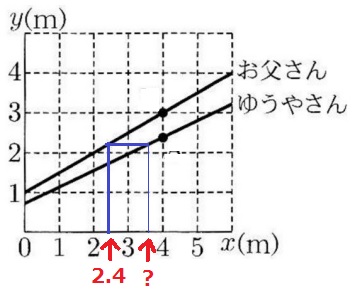
父がｘ＝2.4のときのｙの値を求め、
同じｙの値になるときのゆうやのｘの値を求める。

父は０ｍ地点が1.0ｍ、１ｍごとに0.5ｍずつ長くなる。
【ｙ＝0.5ｘ＋1.0】
ｘ＝2.4を代入して、ｙ＝0.5×2.4＋1.0＝2.2

ゆうやは０ｍ地点が0.8ｍ、１ｍごとに0.4ｍずつ長くなる。
【ｙ＝0.4ｘ＋0.8】
ｙ＝2.2を代入して、2.2＝0.4ｘ＋0.8
ｘ＝3.5　→3.5ｍ

大問10（関数）

（１）　45％
『制動距離は速さの２乗に比例する』→ｙ＝ａｘ²の形。
ｙ＝ａｘ²に（ｘ、ｙ）＝（５、0.1）を代入する。
0.1＝25ａ
ａ＝0.1/25＝１/250

（２）　21％！
制動距離は１/250ｘ²ｍ。
空走距離は比例だから、ｙ＝ａｘに（ｘ、ｙ）＝（５、0.8）を代入すると、
ａ＝0.8/５＝４/25
ｙ＝４/25ｘ
【停止距離＝制御距離＋空走距離】
8.4＝１/250ｘ²＋４/25ｘ　←両辺を250倍
ｘ²＋40ｘ＝2100
ｘ²＋40ｘ－2100
＝（ｘ＋70）（ｘ－30）＝０
ｘ＞０よりｘ＝30
したがって、30ｋｍ/ｈ。

大問11（確率）

（１）　64％
答案では確率を使って説明する。
おのおのの確率を提示して比較すれば足りる。

こういう表を見たことないかな？
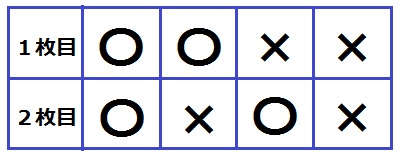
表を〇、裏を×とすると、すべての場合は４通り。
このうち、２枚とも表（〇〇）は１通り、
１枚が表で１枚が裏（〇×、×〇）は２通りある。
確率は１/４と１/２で異なるので、起こりやすさは同じとはいえない。

（２）　57％
いかに時間をかけずに処理するか。。

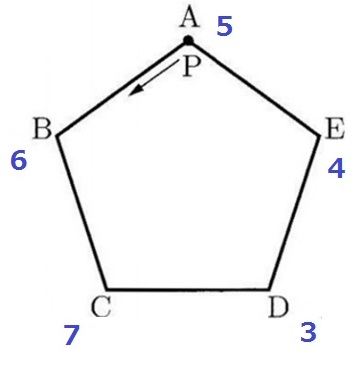
１～４のうち２枚のカードをひく。
同じ数字は重複しないので、最小値は１＋２＝３、最大値は３＋４＝７
Ａから反時計回りに３進むとＤ。７まで進むとＣで終わる。
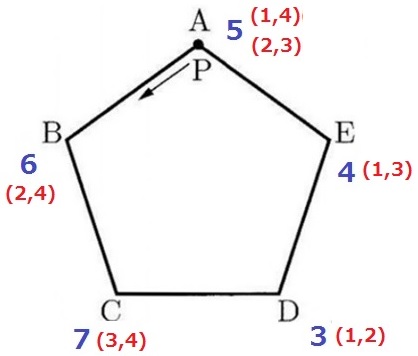
あとは同じ数が重複しないように１～４に分解する。
最も場合の数が大きいのはＡ。確率は２/６＝１/３。

大問12（空間図形）

（１）　59％
ＥＭ＝６÷２＝３ｃｍ
△ＢＥＭで三平方→ＢＭ＝３√10ｃｍ

（２）　１％!!

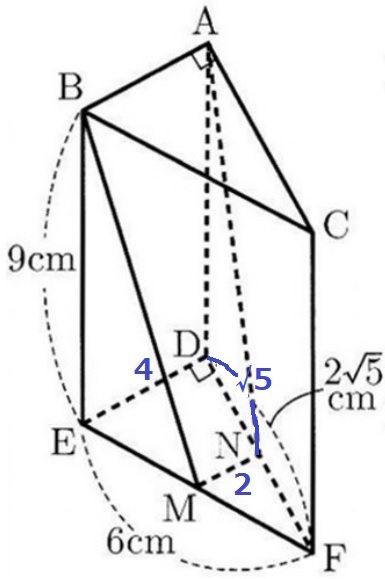
△ＤＥＦで三平方→ＥＤ＝４ｃｍ
ＭとＮは中点→中点連結定理より、ＭＮ＝４÷２＝２ｃｍ
ＤＮ＝２√５÷２＝√５ｃｍ

求積すべき立体がややこしい形をしている。
直角を利用して、立体をうまく分割できないものか。

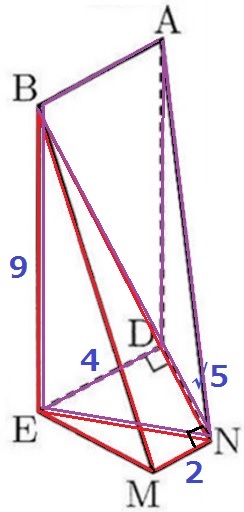
面ＢＮＥで分割する。
四角錐Ｎ－ＡＢＥＤ…底面は長方形ＡＢＥＤ、高さはＤＮ。
　４×９×√５÷３＝12√５ｃｍ³
三角錐Ｂ―ＥＭＮ…中点連結定理からＥＤ//ＭＮで、∠ＤＮＭ＝90°である。
底面は△ＥＭＮ、高さはＢＥ。２×√５÷２×９÷３＝３√５ｃｍ³
したがって、求積すべき立体の体積は、12√５＋３√５＝15√５ｃｍ³

大問数が多いタイムアタック形式。
大問１～５
小問集合でまとめられるくらいの基本問題ゆえ、ミスなくいきたい。
ここまでで44点もある。
４（３）誤答をはじくより、正答を検証した方が早い。
誤答かどうか迷ったら保留することも大事。
大問６
エ：計算しないでヒストグラムに１組を書いてしまう方が早かった。
大問７～８
ここも基本レベル。難しくはない。
大問９
（２）一次方程式の交点座標ではなく、ｙ座標が等しくなるときのゆうやのｘ座標を求める。
2.4地点での父の影の長さ→同じ影の長さになるゆうやの地点。
大問10
（１）を落とすと（２）も落とす。数値の処理はしっかり！
（２）空走距離と制動距離をｘであらわす。
大問11
（２）ちょっと考えて無理そうなら後回し。
大問12
（２）下側に延長して角錐台を求め、三角柱からひいてもできる。
本問は必要な数値がそろっているので、立体を分割して直接求めにいける。

公式にあった設問ごとの正答率の詳細です。